2025年练习生高中数学选择性必修第二册人教B版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年练习生高中数学选择性必修第二册人教B版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
25. [2023·河南焦作高二期中]已知随机变量 $ X $ 的数学期望 $ E(X) = 1 $,方差 $ D(X) = \dfrac{4}{3} $,若随机变量 $ Y $ 满足 $ Y = 3X - 2 $,则 (
A.$ E(Y) = 3, D(Y) = 12 $
B.$ E(Y) = 1, D(Y) = 12 $
C.$ E(Y) = 3, D(Y) = 4 $
D.$ E(Y) = 1, D(Y) = 4 $
B
)A.$ E(Y) = 3, D(Y) = 12 $
B.$ E(Y) = 1, D(Y) = 12 $
C.$ E(Y) = 3, D(Y) = 4 $
D.$ E(Y) = 1, D(Y) = 4 $
答案:
25. B 【解析】因为随机变量$X$的数学期望$E(X)=1$,方差$D(X)=\frac{4}{3}$,所以$E(Y)=E(3X - 2)=3E(X)-2 = 1$,$D(Y)=D(3X - 2)=9D(X)=12$。故选B。
易错规避 $E(aX + b)=aE(X)+b$,$D(aX + b)=a^{2}D(X)$,不要将期望与方差的公式弄混。
易错规避 $E(aX + b)=aE(X)+b$,$D(aX + b)=a^{2}D(X)$,不要将期望与方差的公式弄混。
26. [2023·广西桂林高三月考]已知随机变量 $ X $ 的分布列如下,其中 $ 0 < a < 1 $,则当 $ a $ 在 $ (0, 1) $ 上增大时 (
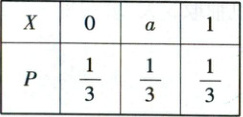
A.$ E(X) $ 不变
B.$ E(X) $ 减小
C.$ D(X) $ 先增大后减小
D.$ D(X) $ 先减小后增大
D
)
A.$ E(X) $ 不变
B.$ E(X) $ 减小
C.$ D(X) $ 先增大后减小
D.$ D(X) $ 先减小后增大
答案:
26. D 【解析】[破题关键:根据分布列写出$E(X)$和$D(X)$关于$a$的函数式,再由函数性质求解]由题意,得$E(X)=0×\frac{1}{3}+a×\frac{1}{3}+1×\frac{1}{3}=\frac{a + 1}{3}$,$D(X)=\left(\frac{a + 1}{3}\right)^{2}×\frac{1}{3}+\left(a - \frac{a + 1}{3}\right)^{2}×\frac{1}{3}+\left(1 - \frac{a + 1}{3}\right)^{2}×\frac{1}{3}=\frac{1}{27}\left[(a + 1)^{2}+(2a - 1)^{2}+(a - 2)^{2}\right]=\frac{2}{9}(a^{2}-a + 1)=\frac{2}{9}\left(a - \frac{1}{2}\right)^{2}+\frac{1}{6}$。当$a$在$(0,1)$上增大时,$E(X)$增大,$D(X)$先减小后增大。故选D。
27. [2023·江苏苏州常熟中学高三期末]设随机变量 $ X \sim B(18, p) $,若 $ D(X) \geq 4 $,则 $ p $ 的取值范围为
$[\frac{1}{3},\frac{2}{3}]$
.
答案:
27. $\left[\frac{1}{3},\frac{2}{3}\right]$ 【解析】由题意知,$X\sim B(18,p)$,则$D(X)=np(1 - p)=18p(1 - p)$。由$D(X)\geq4$,得$18p(1 - p)\geq4$,整理,得$9p^{2}-9p + 2\leq0$,解得$\frac{1}{3}\leq p\leq\frac{2}{3}$。
28. [2023·北京高二期末]已知 $ x, y, z \in \mathbf{N}_+ $,且 $ x + y + z = 10 $,记随机变量 $ \xi $ 为 $ x, y, z $ 中的最大值,则 $ E(\xi) = $
$\frac{17}{3}$
.
答案:
28. $\frac{17}{3}$ 【解析】由题意可得,$\xi$的所有可能取值为$4,5,6,7,8$。利用隔板法可得事件总情况有$\mathrm{C}_{9}^{2}=36$(种)。若$\xi = 4$,三个正整数为$3,3,4$或$2,4,4$,则有$\mathrm{C}_{3}^{1}+\mathrm{C}_{3}^{2}=6$(种)情况,故$P(\xi = 4)=\frac{6}{36}=\frac{1}{6}$;若$\xi = 5$,三个正整数为$1,4,5$或$2,3,5$,则有$\mathrm{A}_{3}^{3}+\mathrm{A}_{3}^{3}=12$(种)情况,故$P(\xi = 5)=\frac{12}{36}=\frac{1}{3}$;若$\xi = 6$,三个正整数为$1,3,6$或$2,2,6$,则有$\mathrm{A}_{3}^{3}+\mathrm{C}_{3}^{1}=9$(种)情况,故$P(\xi = 6)=\frac{9}{36}=\frac{1}{4}$;若$\xi = 7$,三个正整数为$1,2,7$,则有$\mathrm{A}_{3}^{3}=6$(种)情况,故$P(\xi = 7)=\frac{6}{36}=\frac{1}{6}$;若$\xi = 8$,三个正整数为$1,1,8$,则有$\mathrm{C}_{3}^{1}=3$(种)情况,故$P(\xi = 8)=\frac{3}{36}=\frac{1}{12}$。故$\xi$的分布列为
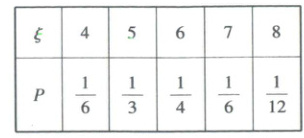
故$E(\xi)=4×\frac{1}{6}+5×\frac{1}{3}+6×\frac{1}{4}+7×\frac{1}{6}+8×\frac{1}{12}=\frac{17}{3}$。
28. $\frac{17}{3}$ 【解析】由题意可得,$\xi$的所有可能取值为$4,5,6,7,8$。利用隔板法可得事件总情况有$\mathrm{C}_{9}^{2}=36$(种)。若$\xi = 4$,三个正整数为$3,3,4$或$2,4,4$,则有$\mathrm{C}_{3}^{1}+\mathrm{C}_{3}^{2}=6$(种)情况,故$P(\xi = 4)=\frac{6}{36}=\frac{1}{6}$;若$\xi = 5$,三个正整数为$1,4,5$或$2,3,5$,则有$\mathrm{A}_{3}^{3}+\mathrm{A}_{3}^{3}=12$(种)情况,故$P(\xi = 5)=\frac{12}{36}=\frac{1}{3}$;若$\xi = 6$,三个正整数为$1,3,6$或$2,2,6$,则有$\mathrm{A}_{3}^{3}+\mathrm{C}_{3}^{1}=9$(种)情况,故$P(\xi = 6)=\frac{9}{36}=\frac{1}{4}$;若$\xi = 7$,三个正整数为$1,2,7$,则有$\mathrm{A}_{3}^{3}=6$(种)情况,故$P(\xi = 7)=\frac{6}{36}=\frac{1}{6}$;若$\xi = 8$,三个正整数为$1,1,8$,则有$\mathrm{C}_{3}^{1}=3$(种)情况,故$P(\xi = 8)=\frac{3}{36}=\frac{1}{12}$。故$\xi$的分布列为

故$E(\xi)=4×\frac{1}{6}+5×\frac{1}{3}+6×\frac{1}{4}+7×\frac{1}{6}+8×\frac{1}{12}=\frac{17}{3}$。
29. [2023·江苏南京外国语学校高二期中]某工厂有甲、乙、丙三条生产线同时生产同一产品,这三条生产线生产产品的次品率分别为 $ 6\% $,$ 5\% $,$ 4\% $,假设这三条生产线产品产量之比为 $ 2:3:5 $,现从这三条生产线上随机任意选取 $ 100 $ 件产品,则次品数的数学期望为
4.7
.
答案:
29. 4.7 【解析】记事件$B$为“选取的产品为次品”,事件$A_{1}$为“此件产品来自甲生产线”,事件$A_{2}$为“此件产品来自乙生产线”,事件$A_{3}$为“此件产品来自丙生产线”。由题意可得$P(A_{1})=\frac{2}{10}=\frac{1}{5}$,$P(A_{2})=\frac{3}{10}$,$P(A_{3})=\frac{5}{10}=\frac{1}{2}$,$P(B|A_{1})=0.06=\frac{3}{50}$,$P(B|A_{2})=0.05=\frac{1}{20}$,$P(B|A_{3})=0.04=\frac{1}{25}$。由全概率公式可得$P(B)=P(A_{1})P(B|A_{1})+P(A_{2})P(B|A_{2})+P(A_{3})P(B|A_{3})=\frac{1}{5}×\frac{3}{50}+\frac{3}{10}×\frac{1}{20}+\frac{1}{2}×\frac{1}{25}=\frac{12 + 15 + 20}{1000}=\frac{47}{1000}$(利用全概率公式求出次品率),即从这三条生产线上随机任意选取1件产品为次品的概率为$\frac{47}{1000}$,则任意选取100件产品,设次品数为$X$,则$X\sim B\left(100,\frac{47}{1000}\right)$,故$E(X)=100×\frac{47}{1000}=4.7$。
30. [2023·江西抚州临川一中高二阶段练习]在棱长为 $ 1 $ 的正方体 $ ABCD - A_1B_1C_1D_1 $ 的 $ 8 $ 个顶点中随机选取 $ 4 $ 个构成一个四面体,记该四面体的体积为 $ V $,则 $ E(V) = $
$\frac{5}{29}$
.
答案:
30. $\frac{5}{29}$ 思维路径 在正方体的8个顶点中随机选取4个点,共有$\mathrm{C}_{8}^{4}=70$(种)情况→再分两类求四面体的体积和取法种数→列出分布列→求出数学期望。
【解析】在棱长为1的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的8个顶点中随机选取4个点,共有$\mathrm{C}_{8}^{4}=70$(种)情况,当四点共面时,共有12种情况,此时不构成四面体。当四点不共面时,四面体的体积有以下两种情况:第一种情况是四面体的四点在相对面且异面的对角线上,如图
(1)中的四面体$ACB_{1}D_{1}$,其体积为$1 - 4×\frac{1}{6}=\frac{1}{3}$,这样的取法共有2种;

第二种情况是四面体的四点中有三个点在一个侧面上,另一个点在相对的侧面上,如图
(2)中的四面体$B_{1}ABC$,其体积为$\frac{1}{6}$,这样的取法共有$70 - 12 - 2 = 56$(种)。所以该四面体的体积$V$的分布列如下:

所以$E(V)=\frac{1}{3}×\frac{1}{29}+\frac{1}{6}×\frac{28}{29}=\frac{5}{29}$。
30. $\frac{5}{29}$ 思维路径 在正方体的8个顶点中随机选取4个点,共有$\mathrm{C}_{8}^{4}=70$(种)情况→再分两类求四面体的体积和取法种数→列出分布列→求出数学期望。
【解析】在棱长为1的正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的8个顶点中随机选取4个点,共有$\mathrm{C}_{8}^{4}=70$(种)情况,当四点共面时,共有12种情况,此时不构成四面体。当四点不共面时,四面体的体积有以下两种情况:第一种情况是四面体的四点在相对面且异面的对角线上,如图
(1)中的四面体$ACB_{1}D_{1}$,其体积为$1 - 4×\frac{1}{6}=\frac{1}{3}$,这样的取法共有2种;

第二种情况是四面体的四点中有三个点在一个侧面上,另一个点在相对的侧面上,如图
(2)中的四面体$B_{1}ABC$,其体积为$\frac{1}{6}$,这样的取法共有$70 - 12 - 2 = 56$(种)。所以该四面体的体积$V$的分布列如下:

所以$E(V)=\frac{1}{3}×\frac{1}{29}+\frac{1}{6}×\frac{28}{29}=\frac{5}{29}$。
31. [2023·浙江金丽衢十二校高三联考]袋中有形状、大小相同的球 $ 5 $ 个,其中红球 $ 3 $ 个,黄球 $ 2 $ 个,现从中随机连续不放回摸球,每次摸 $ 1 $ 个,当两种颜色的球都被摸到时停止摸球,记随机变量 $ \xi $ 为此时已摸球的次数,则 $ E(\xi) = $
$\frac{5}{2}$
.
答案:
31. $\frac{5}{2}$ 【解析】由题意可得$\xi = 2,3,4$,若2次摸到两种颜色的球,则$P(\xi = 2)=\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{3}^{1}\mathrm{C}_{2}^{2}}{\mathrm{C}_{5}^{1}\mathrm{C}_{4}^{1}\mathrm{C}_{3}^{1}}=\frac{3}{5}$;若3次摸到两种颜色的球,则$P(\xi = 3)=\frac{\mathrm{A}_{3}^{2}\mathrm{C}_{3}^{1}+\mathrm{A}_{3}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{5}^{1}\mathrm{C}_{4}^{1}\mathrm{C}_{3}^{1}\mathrm{C}_{2}^{1}}=\frac{3}{10}$;若4次摸到两种颜色的球,则$P(\xi = 4)=\frac{\mathrm{A}_{3}^{3}\mathrm{C}_{2}^{1}}{\mathrm{C}_{5}^{1}\mathrm{C}_{4}^{1}\mathrm{C}_{3}^{1}\mathrm{C}_{2}^{1}}=\frac{1}{10}$。故$E(\xi)=2×\frac{3}{5}+3×\frac{3}{10}+4×\frac{1}{10}=\frac{5}{2}$。
32. [2023·安徽宿州泗县第一中学高二期末]某市拟建立一个博物馆,采取竞标的方式从多家建筑公司中选取一家建筑公司,经过层层筛选,甲、乙两家建筑公司进入最后的招标. 现从建筑设计院聘请专家设计了一个招标方案:两家公司从 $ 6 $ 个招标问题中随机抽取 $ 3 $ 个问题,已知这 $ 6 $ 个招标问题中,甲公司能回答对其中 $ 4 $ 道题目,而乙公司能正确回答每道题目的概率均为 $ \dfrac{2}{3} $,甲、乙两家公司对每道题目的回答都相互独立,互不影响.
(1)求甲公司至少答对 $ 2 $ 道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
(1)求甲公司至少答对 $ 2 $ 道题目的概率;
(2)请从期望和方差的角度分析,甲、乙两家哪家公司竞标成功的可能性更大?
答案:
32. 【解】
(1)由题意可知,甲公司至少答对2道题目可分为答对2题或者答对3道题,
所求概率$p=\frac{\mathrm{C}_{4}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{6}^{3}}+\frac{\mathrm{C}_{4}^{3}}{\mathrm{C}_{6}^{3}}=\frac{4}{5}$。
(2)设甲公司回答正确的题数为$X$,则$X$的可能取值为$1,2,3$($X$服从参数为6,3,4的超几何分布)。
$P(X = 1)=\frac{\mathrm{C}_{4}^{1}\mathrm{C}_{2}^{2}}{\mathrm{C}_{6}^{3}}=\frac{1}{5}$,$P(X = 2)=\frac{\mathrm{C}_{4}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{6}^{3}}=\frac{3}{5}$,$P(X = 3)=\frac{\mathrm{C}_{4}^{3}\mathrm{C}_{2}^{0}}{\mathrm{C}_{6}^{3}}=\frac{1}{5}$。
则$X$的分布列为
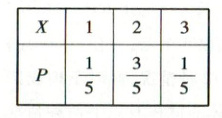
$\therefore E(X)=1×\frac{1}{5}+2×\frac{3}{5}+3×\frac{1}{5}=2$,
$D(X)=(1 - 2)^{2}×\frac{1}{5}+(2 - 2)^{2}×\frac{3}{5}+(3 - 2)^{2}×\frac{1}{5}=\frac{2}{5}$。
设乙公司回答正确的题数为$Y$,则$Y$的取值可能为$0,1,2,3$($Y$服从参数为3,$\frac{2}{3}$的二项分布)。
$P(Y = 0)=\frac{1}{27}$,$P(Y = 1)=\mathrm{C}_{3}^{1}×\frac{2}{3}×\left(\frac{1}{3}\right)^{2}=\frac{2}{9}$,$P(Y = 2)=\mathrm{C}_{3}^{2}×\left(\frac{2}{3}\right)^{2}×\frac{1}{3}=\frac{4}{9}$,$P(Y = 3)=\left(\frac{2}{3}\right)^{3}=\frac{8}{27}$,
则$Y$的分布列为
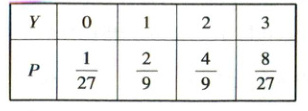
$\therefore E(Y)=0×\frac{1}{27}+1×\frac{2}{9}+2×\frac{4}{9}+3×\frac{8}{27}=2$。
$D(Y)=(0 - 2)^{2}×\frac{1}{27}+(1 - 2)^{2}×\frac{2}{9}+(2 - 2)^{2}×\frac{4}{9}+(3 - 2)^{2}×\frac{8}{27}=\frac{2}{3}$。
由$E(X)=E(Y)$,$D(X)<D(Y)$可得,甲公司竞标成功的可能性更大。
32. 【解】
(1)由题意可知,甲公司至少答对2道题目可分为答对2题或者答对3道题,
所求概率$p=\frac{\mathrm{C}_{4}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{6}^{3}}+\frac{\mathrm{C}_{4}^{3}}{\mathrm{C}_{6}^{3}}=\frac{4}{5}$。
(2)设甲公司回答正确的题数为$X$,则$X$的可能取值为$1,2,3$($X$服从参数为6,3,4的超几何分布)。
$P(X = 1)=\frac{\mathrm{C}_{4}^{1}\mathrm{C}_{2}^{2}}{\mathrm{C}_{6}^{3}}=\frac{1}{5}$,$P(X = 2)=\frac{\mathrm{C}_{4}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{6}^{3}}=\frac{3}{5}$,$P(X = 3)=\frac{\mathrm{C}_{4}^{3}\mathrm{C}_{2}^{0}}{\mathrm{C}_{6}^{3}}=\frac{1}{5}$。
则$X$的分布列为

$\therefore E(X)=1×\frac{1}{5}+2×\frac{3}{5}+3×\frac{1}{5}=2$,
$D(X)=(1 - 2)^{2}×\frac{1}{5}+(2 - 2)^{2}×\frac{3}{5}+(3 - 2)^{2}×\frac{1}{5}=\frac{2}{5}$。
设乙公司回答正确的题数为$Y$,则$Y$的取值可能为$0,1,2,3$($Y$服从参数为3,$\frac{2}{3}$的二项分布)。
$P(Y = 0)=\frac{1}{27}$,$P(Y = 1)=\mathrm{C}_{3}^{1}×\frac{2}{3}×\left(\frac{1}{3}\right)^{2}=\frac{2}{9}$,$P(Y = 2)=\mathrm{C}_{3}^{2}×\left(\frac{2}{3}\right)^{2}×\frac{1}{3}=\frac{4}{9}$,$P(Y = 3)=\left(\frac{2}{3}\right)^{3}=\frac{8}{27}$,
则$Y$的分布列为

$\therefore E(Y)=0×\frac{1}{27}+1×\frac{2}{9}+2×\frac{4}{9}+3×\frac{8}{27}=2$。
$D(Y)=(0 - 2)^{2}×\frac{1}{27}+(1 - 2)^{2}×\frac{2}{9}+(2 - 2)^{2}×\frac{4}{9}+(3 - 2)^{2}×\frac{8}{27}=\frac{2}{3}$。
由$E(X)=E(Y)$,$D(X)<D(Y)$可得,甲公司竞标成功的可能性更大。
查看更多完整答案,请扫码查看


