《2025年练习生高中数学选择性必修第二册人教B版》

1. 已知甲、乙两名员工分别从家中赶往工作单位所用时间互不影响，经统计，甲、乙一个月内从家中到工作单位所用时间在各个时间段内的频率如下：

某日工作单位接到一项任务，需要甲在30min内到达，乙在40min内到达，用X表示甲、乙两人在要求时间内从家中到达单位的人数，用频率估计概率，则X的数学期望和方差分别是(D)

A.$ E(X)=1.5 $，$ D(X)=0.36 $
B.$ E(X)=1.4 $，$ D(X)=0.36 $
C.$ E(X)=1.5 $，$ D(X)=0.34 $
D.$ E(X)=1.4 $，$ D(X)=0.34 $

答案： 1. D 【解析】设事件$ A $表示甲在规定的时间内到达，$ B $表示乙在规定的时间内到达，则$ P(A)=0.5 $，$ P(B)=0.9 $，且$ A,B $相互独立，$\therefore P(X = 0)=P(\overline{A}\overline{B})=P(\overline{A})P(\overline{B})=(1 - 0.5)×(1 - 0.9)=0.05 $，$ P(X = 1)=P(\overline{A}B)+P(A\overline{B})=P(\overline{A})P(B)+P(A)P(\overline{B})=(1 - 0.5)×0.9 + 0.5×(1 - 0.9)=0.5 $，$ P(X = 2)=P(AB)=P(A)P(B)=0.5×0.9 = 0.45 $，$\therefore E(X)=0×0.05 + 1×0.5 + 2×0.45 = 1.4 $。$\because E(X^{2})=0×0.05 + 1×0.5 + 4×0.45 = 2.3 $，$\therefore D(X)=E(X^{2})-E^{2}(X)=0.34 $。故选 D。

2. [2023·河北邯郸高二期中]甲、乙两人进行羽毛球比赛，现采用三局两胜的比赛制度，规定每局比赛都没有平局(必须分出胜负)，且每一局甲赢的概率都是p，随机变量X表示最终的比赛局数，若X的数学期望为$\frac{22}{9}$，则$ p= $(D)

A.$\frac{1}{4}$
B.$\frac{1}{2}$
C.$\frac{3}{4}$
D.$\frac{1}{3}$或$\frac{2}{3}$

答案：
2. D 【解析】随机变量$ X $可能的取值为$ 2,3 $。$ P(X = 2)=\mathrm{C}_{2}^{2}p^{2}+\mathrm{C}_{2}^{2}(1 - p)^{2}=2p^{2}-2p + 1 $，$ P(X = 3)=\mathrm{C}_{2}^{1}(1 - p)p^{2}+\mathrm{C}_{2}^{1}p(1 - p)^{2}=2p - 2p^{2} $。随机变量$ X $的分布列为

故$ E(X)=2×(2p^{2}-2p + 1)+3×(2p - 2p^{2})=-2p^{2}+2p + 2 $。由$ -2p^{2}+2p + 2=\frac{22}{9} $（构造关于$ p $的一元二次方程，解方程即可），解得$ p=\frac{1}{3} $或$ p=\frac{2}{3} $。故选 D。

3. [2023·河南洛阳栾川一中高三开学考试]某市有A，B，C，D四个景点，一位游客来该市游览，已知该游客游览A景点的概率为$\frac{2}{3}$，游览B景点，C景点，D景点的概率都是$\frac{1}{2}$，且该游客是否游览这四个景点相互独立. 用随机变量X表示该游客游览的景点个数，下列错误的是(C)

A.该游客至多游览一个景点的概率为$\frac{1}{4}$
B.$ P(X=2)=\frac{3}{8} $
C.$ P(X=4)=\frac{1}{24} $
D.$ E(X)=\frac{13}{6} $

答案： 3. C 【解析】$ X $的所有可能取值为$ 0,1,2,3,4 $。则$ P(X = 0)=\left(1 - \frac{2}{3}\right)\left(1 - \frac{1}{2}\right)\left(1 - \frac{1}{2}\right)\left(1 - \frac{1}{2}\right)=\frac{1}{24} $，$ P(X = 1)=\frac{2}{3}×\left(1 - \frac{1}{2}\right)^{3}+\left(1 - \frac{2}{3}\right)×\mathrm{C}_{3}^{1}×\frac{1}{2}×\left(1 - \frac{1}{2}\right)^{2}=\frac{5}{24} $，所以该游客至多游览一个景点的概率为$ P(X = 0)+P(X = 1)=\frac{1}{24}+\frac{5}{24}=\frac{1}{4} $，故 A 正确。$ P(X = 2)=\frac{2}{3}×\mathrm{C}_{3}^{1}×\frac{1}{2}×\left(1 - \frac{1}{2}\right)^{2}+\left(1 - \frac{2}{3}\right)×\mathrm{C}_{3}^{2}×\left(\frac{1}{2}\right)^{2}×\left(1 - \frac{1}{2}\right)^{1}=\frac{3}{8} $，故 B 正确。$ P(X = 4)=\frac{2}{3}×\left(\frac{1}{2}\right)^{3}=\frac{1}{12} $，故 C 错误。又$ P(X = 3)=\frac{2}{3}×\mathrm{C}_{3}^{2}×\left(\frac{1}{2}\right)^{2}×\left(1 - \frac{1}{2}\right)+\left(1 - \frac{2}{3}\right)×\mathrm{C}_{3}^{3}×\left(\frac{1}{2}\right)^{3}=\frac{7}{24} $，所以$ E(X)=0×\frac{1}{24}+1×\frac{5}{24}+2×\frac{3}{8}+3×\frac{7}{24}+4×\frac{1}{12}=\frac{13}{6} $，故 D 正确。选 C。

4. [2023·浙江宁波高二期中]5位同学各自写了一封祝福信，并把写好的5封信一起放在心愿盒中，然后每人在心愿盒中各取一封，不放回. 设X为恰好取到自己祝福信的人数，则$ E(X)= $1.

答案： 4. 1 【解析】（破题关键：利用古典概型求解）由题意可知，$ X $的所有可能取值为$ 0,1,2,3,5 $。$ P(X = 5)=\frac{1}{\mathrm{A}_{5}^{5}}=\frac{1}{120} $，$ P(X = 3)=\frac{\mathrm{C}_{5}^{3}}{\mathrm{A}_{5}^{5}}=\frac{10}{120}=\frac{1}{12} $，$ P(X = 2)=\frac{2\mathrm{C}_{5}^{2}}{\mathrm{A}_{5}^{5}}=\frac{20}{120}=\frac{1}{6} $，$ P(X = 1)=\frac{9\mathrm{C}_{5}^{1}}{\mathrm{A}_{5}^{5}}=\frac{45}{120}=\frac{3}{8} $，$ P(X = 0)=1 - \frac{1}{120}-\frac{1}{12}-\frac{1}{6}-\frac{3}{8}=\frac{11}{30} $，则$ E(X)=5×\frac{1}{120}+3×\frac{1}{12}+2×\frac{1}{6}+1×\frac{3}{8}=1 $。

5. [2023·福建福州高二期中]某大型超市为答谢各位员工一年来的锐意进取和辛勤努力，拟在年会后，通过摸球抽奖的方式对500位员工进行奖励. 规定：每位员工从一个装有5种面值奖券的箱子中，一次随机摸出2张奖券，奖券上所标的面值之和就是该员工所获得的奖励额.
（1）若箱子中所装的5种面值的奖券中有2张面值为100元，其余3张均为50元，试比较员工获得100元奖励额与获得150元奖励额的概率的大小；
（2）公司对奖励总额的预算是7万元，箱子中所装的5种面值的奖券有两种方案：第一种方案是3张面值30元和2张面值130元；第二种方案是3张面值40元和2张面值110元. 为了尽可能减少公司奖励总额的预算，请问选择哪一种方案比较好？请说明理由.

答案：
5. 【解】
(1)用$ X $表示员工所获得的奖励额。因为$ P(X = 100)=\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{5}^{2}}=\frac{3}{10} $，$ P(X = 150)=\frac{\mathrm{C}_{2}^{1}\mathrm{C}_{3}^{1}}{\mathrm{C}_{5}^{2}}=\frac{3}{5} $，所以$ P(X = 100)\lt P(X = 150) $，故员工获得$ 100 $元奖励额的概率小于获得$ 150 $元奖励额的概率。
(2)第一种方案：设员工所获得的奖励额为$ X_{1} $。由题意可知，随机变量$ X_{1} $的可能取值有$ 60,160,260 $，$ P(X_{1} = 60)=\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{5}^{2}}=\frac{3}{10} $，$ P(X_{1} = 160)=\frac{\mathrm{C}_{2}^{1}\mathrm{C}_{3}^{1}}{\mathrm{C}_{5}^{2}}=\frac{3}{5} $，$ P(X_{1} = 260)=\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{5}^{2}}=\frac{1}{10} $，则$ X_{1} $的分布列为

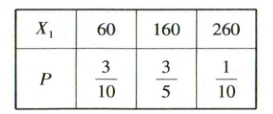
所以$ X_{1} $的数学期望$ E(X_{1})=60×\frac{3}{10}+160×\frac{3}{5}+260×\frac{1}{10}=140 $。
第二种方案：设员工所获得的奖励额为$ X_{2} $。由题意可知，随机变量$ X_{2} $的可能取值有$ 80,150,220 $，$ P(X_{2} = 80)=\frac{\mathrm{C}_{3}^{2}}{\mathrm{C}_{5}^{2}}=\frac{3}{10} $，$ P(X_{2} = 150)=\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{2}^{1}}{\mathrm{C}_{5}^{2}}=\frac{3}{5} $，$ P(X_{2} = 220)=\frac{\mathrm{C}_{2}^{2}}{\mathrm{C}_{5}^{2}}=\frac{1}{10} $，则$ X_{2} $的分布列为

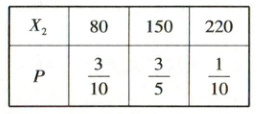
所以$ X_{2} $的数学期望$ E(X_{2})=80×\frac{3}{10}+150×\frac{3}{5}+220×\frac{1}{10}=136 $，$ 500E(X_{2})=68000\lt70000 = 500E(X_{1}) $，所以两种方案都符合要求，但第二种方案的预算更少，故应选择第二种方案。
$\boldsymbol{方法总结}$ 利用均值和方差分析解决实际问题的步骤：
(1)离散型随机变量的均值反映了离散型随机变量取值的平均水平，因此，在实际决策问题中，需先计算均值。
(2)在均值相等的情况下计算方差。方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度，通过计算方差，分析一下哪组数据波动较小。
(3)综合得出结论。