《2025年练习生高中数学选择性必修第二册人教B版》

8. [2022·山东滨州邹平第一中学高二期中]一箱中装有6个大小、质地均相同的红球，编号为1，2，3，4，5，6，还有4个大小、质地均相同的黄球，编号为7，8，9，10.现从箱中任取4个球，下列变量服从超几何分布的是(C)

A.取出的最小号码$ X $
B.有放回地取球时，取出的最大号码$ X $
C.取出的红球个数$ X $
D.有放回地取球时，取出的黄球个数$ X $

答案： 8.C【解析】（破题关键：超几何分布要把总体分为两类，再依次选取或不放回抽取）A，B，D选项均不符合超几何分布的定义，无法用超几何分布的数学模型计算概率，故A，B，D错误；对于C，将红球个数视作正品数，黄球个数视作次品数，则可以用超几何分布的数学模型计算概率。故选C。
方法总结：判断一个随机变量是否服从超几何分布，应看三点：
(1)总体是否可分为两类明确的对象；
(2)是否为不放回抽取；
(3)随机变量是否为样本中其中一类个体的个数。

9. [2023·广西桂林高二期末]一批产品共100件，其中有3件不合格品，从中任取5件，则恰有1件不合格品的概率是(A)

A.$ \dfrac{C_{3}^{1}C_{97}^{4}}{C_{100}^{5}} $
B.$ \dfrac{C_{3}^{1}}{C_{100}^{5}} $
C.$ 1-\dfrac{C_{3}^{1}C_{97}^{4}}{C_{100}^{5}} $
D.$ 1-\dfrac{C_{3}^{1}}{C_{100}^{5}} $

答案： 9.A【解析】一批产品共100件，其中有3件不合格品，从中取5件，恰有1件不合格品的取法有$\mathrm{C}_{3}^{1}\mathrm{C}_{97}^{4}$种，故恰有1件不合格品的概率是$\frac{\mathrm{C}_{3}^{1}\mathrm{C}_{97}^{4}}{\mathrm{C}_{100}^{5}}$。选A。

10. [2023·四川成都第七中学高三月考]袋中有6个大小相同的黑球，编号为1，2，3，4，5，6，还有4个大小相同的白球，编号为7，8，9，10.现从中任取4个球，则下列结论正确的是(B)
①取出的最大号码$ X $服从超几何分布；
②取出的黑球个数$ Y $服从超几何分布；
③取出2个白球的概率为$ \dfrac{1}{14} $；
④若取出一个黑球记2分，取出一个白球记1分，则总得分最大的概率为$ \dfrac{1}{14} $.

A.①②
B.②④
C.③④
D.①③④

答案： 10.B【解析】对于①，根据超几何分布的定义，要把总体分为两类，再依次选取（超几何分布必须是总体分为两类），由此可知取出的最大号码$X$不符合超几何分布的定义，无法用超几何分布的数学模型计算概率，故①错误；对于②，取出的黑球个数$Y$符合超几何分布的定义，将黑球视作第一类，白球视作第二类，可以用超几何分布的数学模型计算概率，故②正确；对于③，取出2个白球的概率为$\frac{\mathrm{C}_{6}^{2}\mathrm{C}_{4}^{2}}{\mathrm{C}_{10}^{4}} = \frac{3}{7}$，故③错误；对于④，若取出一个黑球记2分，取出一个白球记1分，则取出四个黑球的总得分最大，所以总得分最大的概率为$\frac{\mathrm{C}_{6}^{4}}{\mathrm{C}_{10}^{4}} = \frac{1}{14}$，故④正确。选B。

11. [2023·广东东莞高三期末]如图，我国古代珠算算具算盘每个档(挂珠的杆)上有7颗算珠，用梁隔开，梁上面2颗叫上珠，下面5颗叫下珠.若从某一档的7颗算珠中任取3颗，记上珠的个数为$ X $，则 $ P(X\geqslant 1)= $(A)


A.$ \dfrac{5}{7} $
B.$ \dfrac{4}{7} $
C.$ \dfrac{2}{7} $
D.$ \dfrac{1}{7} $

答案： 11.A【解】方法一：由题意可知，$X$的所有可能取值为$0, 1, 2$，则$P(X \geq 1) = P(X = 1) + P(X = 2) = \frac{\mathrm{C}_{2}^{1}\mathrm{C}_{5}^{2}}{\mathrm{C}_{7}^{3}} + \frac{\mathrm{C}_{2}^{2}\mathrm{C}_{5}^{1}}{\mathrm{C}_{7}^{3}} = \frac{5}{7}$。故选A。
方法二：由题意可知，$X$的所有可能取值为$0, 1, 2$，则$P(X \geq 1) = 1 - P(X = 0) = 1 - \frac{\mathrm{C}_{5}^{3}}{\mathrm{C}_{7}^{3}} = \frac{5}{7}$。故选A。

12. [2023·广东江门棠下中学高三期末]学校要从5名男教师和2名女教师中随机选出3人去支教，设抽取的3人中女教师的人数为$ X $，则 $ P(X\leqslant 1)= $$\frac{6}{7}$.

答案： 12.$\frac{6}{7}$【解析】由题意可得$P(X = 0) = \frac{\mathrm{C}_{5}^{3}}{\mathrm{C}_{7}^{3}} = \frac{2}{7}$，$P(X = 1) = \frac{\mathrm{C}_{2}^{1}\mathrm{C}_{5}^{2}}{\mathrm{C}_{7}^{3}} = \frac{4}{7}$，所以$P(X \leq 1) = P(X = 0) + P(X = 1) = \frac{2}{7} + \frac{4}{7} = \frac{6}{7}$。

13. [2023·北京东城高二期末]某单位组织知识竞赛，按照比赛规则，每位参赛者从5道备选题中随机抽取3道题作答.假设在5道备选题中，甲答对每道题的概率都是$ \dfrac{2}{3} $，且每道题答对与否互不影响，则甲恰好答对其中2道题的概率为$\frac{4}{9}$；若乙能答对其中3道题且另外2道题不能答对，则乙恰好答对2道题的概率为$\frac{3}{5}$.

答案： 13.$\frac{4}{9}$ $\frac{3}{5}$【解析】（破题关键：甲答对题目数量$X$服从二项分布；乙答对题目数量$Y$服从超几何分布）设甲能够答对$X$道题目，则$X \sim B\left(3, \frac{2}{3}\right)$，所以$P(X = 2) = \mathrm{C}_{3}^{2} × \left(\frac{2}{3}\right)^{2} × \left(1 - \frac{2}{3}\right) = \frac{4}{9}$。假设乙能够答对$Y$道题目，则$Y \sim H(5, 3, 3)$，所以$P(Y = 2) = \frac{\mathrm{C}_{3}^{2}\mathrm{C}_{2}^{1}}{\mathrm{C}_{5}^{3}} = \frac{3}{5}$。

14. 某市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了考核，记考核成绩不小于80分的为优秀.为了了解本次培训活动的效果，在参加培训的学生中随机抽取了60名学生的考核成绩，如下表：

(1)从参加培训的学生中随机选取1人，请根据表中数据，估计这名学生考核优秀的概率；
(2)用分层抽样的方法，在考核成绩为$ [70,90) $的学生中任取8人，再从这8人中随机选取4人，记取到考核成绩在$ [80,90) $的学生人数为$ X $，求$ X $的分布列.

答案：
14.【解】
(1)设该名学生考核优秀为事件$A$。由已知的60名学生的成绩，知成绩优秀的有35名学生，所以$P(A) = \frac{35}{60} = \frac{7}{12}$，因此可估计这名学生考核优秀的概率为$\frac{7}{12}$。
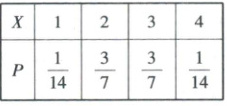
(2)由已知得，用分层抽样的方法，在考核成绩为$[70, 90)$的学生中任取8人，则考核成绩在$[70, 80)$的学生应抽取3人，考核成绩在$[80, 90)$的学生应抽取5人（分层抽样的抽样比相同）。由题意可得$X$的所有可能取值为$1, 2, 3, 4$（$X$服从超几何分布），所以$P(X = 1) = \frac{\mathrm{C}_{3}^{3}\mathrm{C}_{5}^{1}}{\mathrm{C}_{8}^{4}} = \frac{1}{14}$，$P(X = 2) = \frac{\mathrm{C}_{3}^{2}\mathrm{C}_{5}^{2}}{\mathrm{C}_{8}^{4}} = \frac{3}{7}$，$P(X = 3) = \frac{\mathrm{C}_{3}^{1}\mathrm{C}_{5}^{3}}{\mathrm{C}_{8}^{4}} = \frac{3}{7}$，$P(X = 4) = \frac{\mathrm{C}_{3}^{0}\mathrm{C}_{5}^{4}}{\mathrm{C}_{8}^{4}} = \frac{1}{14}$。所以随机变量$X$的分布列为

方法总结：解决超几何分布问题的两个关键点：
(1)超几何分布是概率分布的一种形式，一定要注意公式中字母的范围及其意义，解决问题时可以直接利用公式求解，但不能机械记忆。
(2)超几何分布中，只要知道$M, N, n$就可以利用公式求出$X$取不同$k$值的概率，从而求出$X$的分布列。