2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
21. (8分)
利用全等三角形面积相等可以解决与图形面积相关的问题.
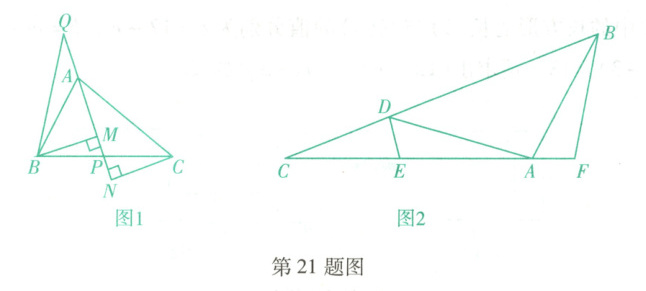
如图1,在$\triangle ABC$中,$AP$为中线,过点$B$作$BM \perp AP$于点$M$,过点$C$作$CN \perp AP$交$AP$的延长线于点$N$.在$PA$的延长线上取一点$Q$,连接$BQ$,使$\angle Q = \angle CAN$.
(1)比较$S_{\triangle BMP}$和$S_{\triangle CNP}$的大小.
(2)试说明$S_{\triangle QBM} = S_{\triangle BMP} + S_{\triangle ACP}$.
(3)如图2,在$\triangle ABC$中,$\angle BAC$是钝角,点$D$在边$BC$上,$AB = DA$,点$E$在边$AC$上,点$F$在边$CA$的延长线上,$\angle BAF > \angle DAE$,$\angle BFA = \angle AED = \angle BAD$.若$BD = 2DC$,$\triangle ABD$的面积是12,求$\triangle ABF$与$\triangle CDE$的面积之和.
利用全等三角形面积相等可以解决与图形面积相关的问题.
如图1,在$\triangle ABC$中,$AP$为中线,过点$B$作$BM \perp AP$于点$M$,过点$C$作$CN \perp AP$交$AP$的延长线于点$N$.在$PA$的延长线上取一点$Q$,连接$BQ$,使$\angle Q = \angle CAN$.
(1)比较$S_{\triangle BMP}$和$S_{\triangle CNP}$的大小.
(2)试说明$S_{\triangle QBM} = S_{\triangle BMP} + S_{\triangle ACP}$.
(3)如图2,在$\triangle ABC$中,$\angle BAC$是钝角,点$D$在边$BC$上,$AB = DA$,点$E$在边$AC$上,点$F$在边$CA$的延长线上,$\angle BAF > \angle DAE$,$\angle BFA = \angle AED = \angle BAD$.若$BD = 2DC$,$\triangle ABD$的面积是12,求$\triangle ABF$与$\triangle CDE$的面积之和.

答案:
21.
(1)解:在△ABC中,AP为中线,
∴BP = CP,
∵BM⊥AP,CN⊥AP,
∴∠BMP = ∠CMP = 90°,又
∵∠BPM = ∠CPN,
∴△BMP ≌ △CNP(AAS),
∴$S_{△BMP} = S_{△CNP}.$
(2)证明:
∵AP为中线,
∴BP = CP,
∵BM⊥AP,CN⊥AP,
∴∠BMP = ∠CNP = 90°,又
∵∠BPM = ∠CPN,
∴△BMP ≌ △CNP(AAS),
∴BM = CN,
∵∠BMP = 90°,
∴∠BMQ = ∠CNA = 90°,又
∵∠Q = ∠CAN,
∴△QBM ≌ △ACN(AAS),
∴$S_{△QBM} = S_{△ACN},$
∴$S_{△QBM} = S_{△ACN} = S_{△CNP} + S_{△ACP} = S_{△BMP} + S_{△ACP}.$
(3)解:
∵∠BFA = ∠AED = ∠BAD,∠BAF + ∠DAE = 180° - ∠BAD,∠BAF + ∠ABF = 180° - ∠BFA,
∴∠DAE = ∠ABF,在△ABF和△DAE中,$\begin{cases} ∠BFA = ∠AED, \\ ∠ABF = ∠DAE, \\ AB = DA, \end{cases} $
∴△ABF ≌ △DAE(AAS),
∴$S_{△ABF} = S_{△DAE},$设△ABD的底边BD上的高为h,则△ADC的底边DC上的高为h,
∴$S_{△ABD} = \frac{1}{2}BD·h = 12,$$S_{△ADC} = \frac{1}{2}DC·h,$
∵BD = 2DC,
∴$S_{△ADC} = 6,$
∴$S_{△ADC} = S_{△CDE} + S_{△DAE} = S_{△CDE} + S_{△ABF} = 6,$即△ABF与△CDE的面积之和为6.
(1)解:在△ABC中,AP为中线,
∴BP = CP,
∵BM⊥AP,CN⊥AP,
∴∠BMP = ∠CMP = 90°,又
∵∠BPM = ∠CPN,
∴△BMP ≌ △CNP(AAS),
∴$S_{△BMP} = S_{△CNP}.$
(2)证明:
∵AP为中线,
∴BP = CP,
∵BM⊥AP,CN⊥AP,
∴∠BMP = ∠CNP = 90°,又
∵∠BPM = ∠CPN,
∴△BMP ≌ △CNP(AAS),
∴BM = CN,
∵∠BMP = 90°,
∴∠BMQ = ∠CNA = 90°,又
∵∠Q = ∠CAN,
∴△QBM ≌ △ACN(AAS),
∴$S_{△QBM} = S_{△ACN},$
∴$S_{△QBM} = S_{△ACN} = S_{△CNP} + S_{△ACP} = S_{△BMP} + S_{△ACP}.$
(3)解:
∵∠BFA = ∠AED = ∠BAD,∠BAF + ∠DAE = 180° - ∠BAD,∠BAF + ∠ABF = 180° - ∠BFA,
∴∠DAE = ∠ABF,在△ABF和△DAE中,$\begin{cases} ∠BFA = ∠AED, \\ ∠ABF = ∠DAE, \\ AB = DA, \end{cases} $
∴△ABF ≌ △DAE(AAS),
∴$S_{△ABF} = S_{△DAE},$设△ABD的底边BD上的高为h,则△ADC的底边DC上的高为h,
∴$S_{△ABD} = \frac{1}{2}BD·h = 12,$$S_{△ADC} = \frac{1}{2}DC·h,$
∵BD = 2DC,
∴$S_{△ADC} = 6,$
∴$S_{△ADC} = S_{△CDE} + S_{△DAE} = S_{△CDE} + S_{△ABF} = 6,$即△ABF与△CDE的面积之和为6.
查看更多完整答案,请扫码查看


