《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

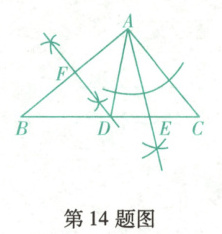
14. (抚顺新宾期末)如图,在$\triangle ABC$中,$\angle B=40^{\circ}$,$\angle C=50^{\circ}$,则$\angle DAE$的度数为25°.

答案： 14.25°　[解析]观察尺规作图的痕迹，可以发现直线DF是线段AB的垂直平分线，射线AE是∠DAC的平分线，
∵DF垂直平分线段AB，
∴DA = DB，
∴∠BAD = ∠B = 40°，
∵∠B = 40°，∠C = 50°，
∴∠BAC = 90°，
∴∠CAD = 50°，
∵AE平分∠CAD，
∴∠DAE = $\frac{1}{2}$∠CAD = 25°.

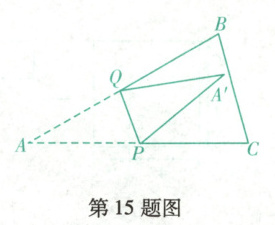
15. (大连沙河口期末)如图的$\triangle ABC$纸片,$\angle A=30^{\circ}$,$P$是$AC$的中点,点$Q$从点$A$出发沿$AB$向点$B$运动,到达点$B$时停止运动.若将$\triangle APQ$沿$PQ$进行对折,点$A$的对应点记为$A'$,设$\angle A'PC=\alpha$,$\angle A'QB=\beta$.当$\alpha＞\beta$时,$\alpha$与$\beta$之间的数量关系为α+β=60°.

答案： 15.α + β = 60°　[解析]
∵∠A = 30°，
∴∠AQP + ∠APQ = 180° - 30° = 150°，由折叠的性质知∠AQP = ∠A'QP，∠APQ = ∠A'PQ，
∵2∠AQP = 180° - ∠A'QB，2∠APQ = 180° - ∠A'PC，
∴2(∠AQP + ∠APQ) = 360° - (∠A'QB + ∠A'PC)，即2×150° = 360° - (α + β)，
∴α + β = 60°.

16. (每小题5分,共10分)(大连高新期末)
计算:
(1)$(2a^{2}-1)(a-4)$;
(2)$(2x+3y)^{2}-(2x+y)(2x-y)$.

答案： 16.解:
(1)原式 = 2$a^3$ - 8$a^2$ - a + 4.
(2)原式 = 4$x^2$ + 12xy + 9$y^2$ - (4$x^2$ - $y^2$) = 4$x^2$ + 12xy + 9$y^2$ - 4$x^2$ + $y^2$ = 12xy + 10$y^2$.

17. (8分)(葫芦岛兴城期末)
先化简,再求值:$(\frac{x^{2}-2x}{x^{2}-1}-1)÷\frac{2x-1}{x+1}$,请在$-2\leq x\leq2$的范围内选择一个合适的整数代入求值.

答案： 17.解:原式 = ($\frac{x^2 - 2x}{x^2 - 1}$ - $\frac{x^2 - 1}{x^2 - 1}$)÷$\frac{2x - 1}{x + 1}$ = $\frac{-2x + 1}{x^2 - 1}$·$\frac{x + 1}{2x - 1}$ = $\frac{1}{1 - x}$，要使原式有意义，则x≠±1，x≠ - $\frac{1}{2}$，故在 - 2≤x ≤2的范围内可选取整数0(或±2)，当x = 0时，原式 = 1.

18. (8分)(葫芦岛连山期末)
某图书馆计划选购甲、乙两种图书.已知甲图书每本价格是乙图书每本价格的2.5倍,用800元单独购买甲图书比用800元单独购买乙图书要少24本.
(1)甲、乙两种图书每本价格分别为多少元?
(2)如果该图书馆计划购买乙种图书的本数比购买甲种图书本数的2倍多8本,且用于购买甲、乙两种图书的总经费不超过1060元,那么该图书馆最多可以购买多少本甲种图书?

答案： 18.解:
(1)设乙种图书每本价格为x元，则甲种图书每本价格是2.5x元，根据题意得$\frac{800}{x}$ - $\frac{800}{2.5x}$ = 24，解得x = 20，经检验，x = 20是原分式方程的解，则2.5x = 50.
答:甲种图书每本50元，乙种图书每本20元.
(2)设购买甲种图书本数为a，则购买乙种图书的本数为2a + 8，根据题意得50a + 20(2a + 8) ≤1060，解得a ≤10.
答:该图书馆最多可以购买10本甲种图书.