《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

18. (8分)(大连中山期末)
如图,在平面直角坐标系$xOy$中,$\triangle AOB$的顶点坐标为$O(0,0)$,$A(-2,1)$,$B(1,2)$.
(1)在图中画出$\triangle AOB$关于$x$轴对称的$\triangle A'OB'$.
(2)在$y$轴上画出点$P$,使得$PA + PA'$的值最小(保留作图痕迹),并直接写出点$P$的坐标.

答案：
18.解:
(1)如答图，△A'OB'即为所求作.
(2)如答图，取点A关于y轴的对称点A"，连接A'A"，交y轴于点P，此时PA+PA'=PA"+PA'=A'A"，为最小值，则点P即为所求作.　点P 的坐标为(0，0).

19. (8分)
"白日登山望烽火,黄昏饮马傍交河",这是唐代诗人李颀《古从军行》里的一句诗,由此却引申出一系列非常有趣的数学问题,通常称为"将军饮马"问题.
(1)如图1,若点$A$和点$B$分别在直线$l$的两侧,请作出示意图,在直线$l$上找到点$C$,使得$CA + CB$有最小值,并说明作图依据.
(2)如图2,若点$A$和点$B$在直线$l$的同侧,请在直线$l$上作出点$P$,使得$PA + PB$有最小值.
(3)如图3,已知$\angle AOB = 30^{\circ}$,点$Q$在$\angle AOB$的内部,点$M,N$分别在射线$OA,OB$上.若$OQ = 6$,请求出$\triangle QMN$周长的最小值.

答案：
19.解:
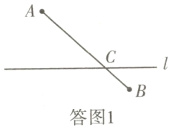
(1)连接AB，与直线l相交于点C，则CA +CB有最小值.作图依据是两点之间线段最短.　如答图1.

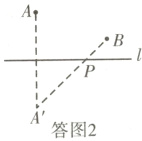
(2)如答图2，点P即为所求作.

(3)作点Q关于OA的对称点C，作点Q关于OB 的对称点D，连接CD，分别交OA于点M，交OB于点N，则△QMN的周长最小，连接OC，OD，如答图3，
∵点C和点Q关于OA对称，
∴OC=OQ=6，∠MOC=∠QOM，同理可得OD =OQ=6，∠QON=∠NOD，
∴OC=OD，∠MOC+∠QOM+∠QON+∠NOD=2∠QOM+2∠QON=2(∠QOM+∠QON)=2∠AOB=60°，
∴△COD为等边三角形，
∴CD=6，
∴△QMN 的周长=QM+MN+QN=CM+MN+DN=CD =6.