《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

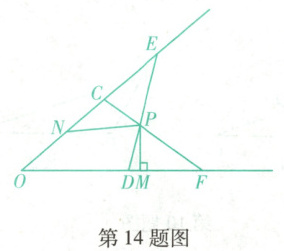
14. (葫芦岛兴城期末)如图,在$\angle AOB$的两边上分别截取$OC = OD$,$OE = OF$(点$C$与点$E$不重合),连接$CF$,$DE$,$CF$与$DE$交于点$P$,过点$P$作$PM \perp OB$,垂足为$M$,$N$是线段$OC$上一点,连接$PN$,且$\angle PNO + \angle PFO = 180^{\circ}$.若$ON = 3$,$OF = 7$,则$OM$的长为5.

答案：
14.5 【解析】如答图，过点P作PQ⊥OA于点Q，在△EOD和△FOC中，$\begin{cases} CE = OF, \\ ∠O = ∠FOC, \\ OD = OC, \end{cases} $
∴△EOD ≌ △FOC(SAS)，
∴∠OED = ∠OFC，
∵OC = OD，OE = OF，
∴CE = DF，在△CPE和△DPF中，$\begin{cases} ∠CPE = ∠DPF, \\ ∠CEP = ∠DFP, \\ CE = DF, \end{cases} $
∴△CPE ≌ △DPF(AAS)，
∴$S_{△CPE} = S_{△DPF}，$PE = PF，
∴$\frac{1}{2}CE·PQ = \frac{1}{2}DF·PM，$
∴PQ = PM，
∵∠PNO + ∠PFO = 180°，∠PNO + ∠PNQ = 180°，
∴∠PNQ = ∠PFO，在△PNQ和△PFM中，$\begin{cases} ∠PNQ = ∠PFM, \\ ∠PQN = ∠PMF = 90°, \\ PQ = PM, \end{cases} $
∴△PNQ ≌ △PFM(AAS)，
∴PN = PF，NQ = FM，
∵PQ⊥NE，
∴$NQ = EQ = \frac{1}{2}EN，$
∵ON = 3，OF = OE = 7，
∴EN = OE - ON = 4，
∴NQ = 2 = FM，
∴OM = OF - FM = 5.

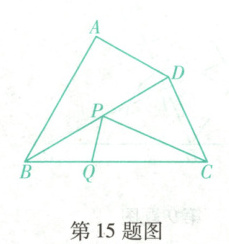
15. (葫芦岛绥中期末)如图,在四边形$ABCD$中,$\angle ABC = 60^{\circ}$,$BD$平分$\angle ABC$,$\angle BCD ＞ \angle CBD$,$BC = 24$,$P$,$Q$分别是$BD$,$BC$上的动点.当$CP + PQ$取得最小值时,$BQ$的长是12.

答案： 15.12 【解析】观察图形特点可知点Q关于直线BD的对称点Q'均在AB上，所以CP + PQ的值可以转化为CP + PQ'，易知由点C向AB作垂线时，CP + PQ'的值最小，为线段CQ'的长度，由Rt△CQ'B中，由∠Q'BC = 60°易知，$BQ' = \frac{1}{2}BC = \frac{1}{2}×24 = 12 = BQ.$

16. (每小题5分,共10分)(铁岭县期末)
计算:
(1)$(- 3a^{2}b^{2}) · (- 2ab)^{2} ÷ (2ab^{2})^{2}$;
(2)$(2x + 1)(2x - 1) - (2x - 3)^{2}$.

答案： 16.解：
(1)原式$ = (-3a^{2}b^{2})·4a^{2}b^{2}÷4a^{2}b^{4} = -12a^{4}b^{4}÷4a^{2}b^{4} = -3a^{2}.$
(2)原式$ = 4x^{2} - 1 - 4x^{2} + 12x - 9 = 12x - 10.$

17. (8分)(大连高新期末)
先化简,再求值:$(\frac{2}{a - 2} - \frac{a^{2} - 4}{a^{2} - 4a + 4}) ÷ \frac{a^{2} + 2a}{a - 2}$,其中$a = - 3$.

答案： 17.解：原式$ = [\frac{2}{a - 2} - \frac{(a + 2)(a - 2)}{(a - 2)^{2}}]·\frac{a - 2}{a(a + 2)} = (\frac{2}{a - 2} - \frac{a - 2}{a - 2})·\frac{a - 2}{a(a + 2)} = \frac{2 - a - 2}{a(a + 2)} = \frac{-a}{a(a + 2)} = -\frac{1}{a + 2}，$当a = -3时，原式$ = -\frac{1}{-3 + 2} = 1.$

18. (8分)(鞍山期末)
为筹办元旦联欢会,八年级(1)班两次到超市购买同一款饮料,第一次按标价购买,用了96元;第二次超市有优惠活动,按标价的6折购买,用了72元.若两次一共购买了60瓶饮料,则这种饮料的标价是多少?

答案： 18.解：设这种饮料的标价是x元/瓶，根据题意得$\frac{96}{x} + \frac{72}{0.6x} = 60，$解得x = 3.6，经检验，x = 3.6是原分式方程的解，且符合题意.
答：这种饮料的标价是3.6元/瓶.