《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

23. （13分）（大连甘井子期末）
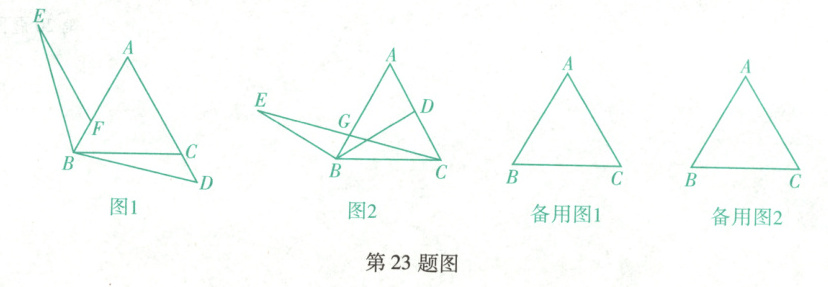
$ \triangle ABC $是等边三角形，$ D $为射线$ AC $上一点，连接$ BD $，$ \angle DBE = 120^{\circ} $，$ BD = BE $.
（1）如图1，过点$ E $作$ EF// AC $交边$ AB $于点$ F $，求证：$ CD = FB $.
（2）如图2，点$ D $在边$ AC $上时，连接$ CE $交边$ AB $于点$ G $. 若$ AB = 4 $，$ BG = 1 $，求证：$ BD\perp AC $.
（3）当点$ D $在$ AC $的延长线上时，连接$ CE $与射线$ BA $交于点$ G $. 若$ \frac{AC}{CD}=k(k\neq 1) $，请直接

写

出

$ \frac{BG}{AG} $的值. （用含$ k $的代数式表示）

答案：
23.
(1)证明:
∵△ABC是等边三角形，
∴∠ABC=∠ACB=∠A=60°,
∴∠BCD=120°,
∵EF//AC,
∴∠EFA=∠A=60°,
∴∠BFE=120°=∠BCD,
∵∠DBE=120°,∠ABC=60°,
∴∠EBF+∠DBC=60°,
∵∠ACB=∠DBC+∠D=60°,
∴∠EBF=∠D,又
∵BE=BD,
∴△EFB≌△BCD(AAS),
∴CD=FB.
(2)证明:过点E作EF//AC交边AB的延长线于点F，如答图1，
∴∠F=∠A=60°,
∵∠ABC=60°,
∴∠FBC=120°,
∵∠DBE=120°,
∴∠CBD+∠EBF=360°−120°−120°=120°,∠ACB=60°,
∴∠CDB+∠CBD=120°,
∴∠EBF=∠CDB,又
∵BD=BE,
∴△EFB≌△BCD(AAS),
∴FB=CD,EF=BC=AC,又
∵∠F=∠A,∠EGF=∠CGA,
∴△EGF≌△CGA(AAS),
∴FG=AG=3,
∵BG=1,
∴FB=2,
∴CD=FB=2,
∵AC=4,
∴AD=AC−CD=4−2=2,
∵△ABC是等边三角形，
∴BD⊥AC.

(3)解:
∵$\frac{AC}{CD}$=k(k≠1),
∴设CD=x,则AC=kx，分两种情况:①当点G在BA的延长线上时，过点E作EF//AC交射线BA于点F,如答图2,同理得△EFB≌△BCD(AAS)，
∴BF=CD=x,EF=BC=AC=kx,同理得△EGF≌△CGA(AAS),
∴FG=AG=$\frac{x-kx}{2}$,
∴$\frac{BG}{AG}$=$\frac{\frac{x-kx}{2}+x}{\frac{x-kx}{2}}$=$\frac{1+k}{1-k}$;②当点G在线段AB上时，过点E作EF//AC交BA于点F,如答图3,同理得△EFB≌△BCD(AAS),
∴BF=CD=x,EF=BC=AC=kx,同理得△EGF≌△CGA(AAS),
∴FG=AG=$\frac{kx-x}{2}$,
∴$\frac{BG}{AG}$=$\frac{kx-x}{\frac{kx-x}{2}}$=$\frac{k+1}{k-1}$.
综上所述，$\frac{BG}{AG}$的值为$\frac{1+k}{1-k}$或$\frac{k+1}{k-1}$.