《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

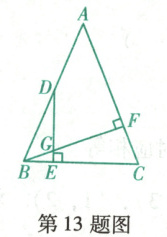
13. (抚顺新宾期末)如图,$ \triangle A B C $是等腰三角形,$ A B=A C $,$ \angle A=45^{\circ} $,在腰$ A B $上取一点$ D $,$ D E \perp B C $,垂足为$ E $,另一腰$ A C $上的高$ B F $交$ D E $于点$ G $,垂足为$ F $.若$ B E=3 $,则$ D G $的长为6.

答案：
13.6　[解析]过点G作MG⊥BF交BD于点M，过点M作NM⊥ED于点N，如答图，
∵AB = AC，∠A = 45°，DE⊥BC，
∴∠ABC = ∠C = 67.5°，∠BDE = 22.5°，∠ABF = ∠A = 45°，
∵∠FBC = 90° - ∠C = 22.5°，
∴∠BGE = 67.5°，
∴∠FBC = ∠BDE，
∵MG⊥BF，NM⊥ED，
∴∠BGM = ∠MND = 90°，∠ABF = ∠BMG = 45°，
∴∠MGD = 180° - ∠BGE - ∠BGM = 22.5°，MG = BG，
∴∠MGD = ∠BDG，
∴MG = DM = BG，DG = 2DN，在△DNM与△BEG中，
$\begin{cases}∠MND = ∠GEB = 90° \\∠BDE = ∠FBC \\DM = BG\end{cases}$
∴△DNM≌△BEG(AAS)，
∴DN = BE = 3，
∴DG = 2DN = 6.

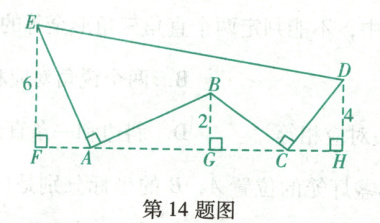
14. (抚顺县期末)如图,$ A E \perp A B $,且$ A E=A B $,$ B C \perp C D $,且$ B C=C D $,请按照图中所标注的数据计算图中实线所围成的图形的面积$ S= $50.

答案： 14.50　[解析]
∵AE⊥AB，EF⊥AF，BG⊥AG，
∴∠F = ∠AGB = ∠EAB = 90°，
∴∠FEA + ∠EAF = 90°，∠EAF + ∠BAG = 90°，
∴∠FEA = ∠BAG，又
∵AE = AB，
∴△FEA≌△GAB(AAS)，
∴AG = EF = 6，AF = BG = 2，同理CG = DH = 4，BG = CH = 2，
∴FH = 2 + 6 + 4 + 2 = 14，
∴梯形EFHD的面积 = $\frac{1}{2}$(EF + DH)·FH = $\frac{1}{2}$×(6 + 4)×14 = 70，
∴实线所围成的图形的面积S = S梯形EFHD - S△EFA - S△ABC - S△DHC = 70 - $\frac{1}{2}$×6×2 - $\frac{1}{2}$×(6 + 4)×2 - $\frac{1}{2}$×4×2 = 50.

15. (大连瓦房店期末)如图,在等边三角形$ A B C $中,$ D $为$ A C $的中点,$ P $,$ Q $分别为$ A B $,$ A D $上的点,$ B P=A Q=3 $,$ Q D=2 $,在$ B D $上有一动点$ E $,则$ P E+Q E $的最小值为7.

答案：
15.7　[解析]
∵△ABC是等边三角形，
∴BA = BC，
∵D为AC的中点，
∴BD⊥AC，
∵AQ = 3，QD = 2，
∴AD = DC = AQ + QD = 5，如答图，作点Q关于BD的对称点Q'，连接PQ'交BD于点E，连接QE，PE + QE = PE + Q'E，当点P，E，Q'共线时，PE + QE的值最小，最小值为PQ'的长，
∵AQ = 3，AD = DC = 5，
∴QD = Q'D = 2，
∴CQ' = BP = 3，
∴AP = AQ' = 7，
∵∠A = 60°，
∴△APQ'是等边三角形，
∴PQ' = AP = 7，
∴PE + QE的最小值为7.

16. (每小题5分,共10分)(抚顺县期末)
计算:
(1)$ \left(2 a^{3}\right)^{3}-\left(a^{3}\right)^{2} · a^{2} · a $;
(2)$ (3 x+1)(x+2) $.

答案： 1. （1）
解：
首先，根据幂的乘方公式$(a^{m})^{n}=a^{mn}$和积的乘方公式$(ab)^{n}=a^{n}b^{n}$计算$(2a^{3})^{3}$：
$(2a^{3})^{3}=2^{3}·(a^{3})^{3}=8a^{9}$。
然后，根据同底数幂的乘法公式$a^{m}· a^{n}=a^{m + n}$计算$(a^{3})^{2}· a^{2}· a$：
$(a^{3})^{2}· a^{2}· a=a^{6}· a^{2}· a=a^{6 + 2+1}=a^{9}$。
最后，计算$(2a^{3})^{3}-(a^{3})^{2}· a^{2}· a$：
$8a^{9}-a^{9}=(8 - 1)a^{9}=7a^{9}$。
2. （2）
解：
根据多项式乘多项式法则$(a + b)(c + d)=ac+ad+bc+bd$计算$(3x + 1)(x + 2)$：
$(3x + 1)(x + 2)=3x· x+3x·2+1· x+1×2$。
由同底数幂的乘法公式$a^{m}· a^{n}=a^{m + n}$（这里$a = x$，$m=n = 1$时，$x· x=x^{2}$）可得：
$3x· x+3x·2+1· x+1×2=3x^{2}+6x+x + 2$。
合并同类项：$3x^{2}+(6x+x)+2=3x^{2}+7x + 2$。
综上，（1）的结果是$7a^{9}$；（2）的结果是$3x^{2}+7x + 2$。

17. (8分)(营口鲅鱼圈期末)
先化简,后求值:$ \left(\frac{1}{x-2}+x-4\right) ÷ \frac{x^{2}-6 x+9}{x^{2}-4} $,其中$ x=-5 $.

答案：

17.解:原式=$\left(\frac{1}{x-2}+\frac{(x-4)(x-2)}{x-2}\right)÷\frac{x^{2}-6x+9}{x^{2}-4}$

=$\frac{1+x^{2}-6x+8}{x-2}÷\frac{(x-3)^{2}}{(x+2)(x-2)}$

=$\frac{x^{2}-6x+9}{x-2}·\frac{(x+2)(x-2)}{(x-3)^{2}}$

=$\frac{(x-3)^{2}}{x-2}·\frac{(x+2)(x-2)}{(x-3)^{2}}$

=$x+2$

当$x=-5$时，原式=$-5+2=-3$