《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

22. (12分)(大连沙河口期末)
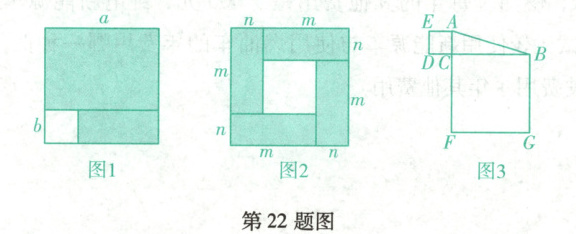
在数学学习中,图表有着重要的作用,它能将复杂或抽象的问题直观化,用图表的直观来描述、解释问题,用图表的解释来分析、解决问题,例如,平方差公式就可以利用图形来直观描述并解释.如图1,在边长为a的正方形中剪去一个边长为b的正方形$(a ＞ b)$,若用两种不同的方法来表示阴影部分的面积,就能得到公式$(a + b)(a - b) = a^{2} - b^{2}$.如图2,用4张形状、大小相同的长方形纸片拼成一个大正方形,已知长方形的长、宽分别为m,n$(m ＞ n)$.
(1)观察图2,写出$(m + n)^{2}$,$(m - n)^{2}$和mn之间的数量关系并用整式的运算说明.
(2)如图3,在$Rt\triangle ABC$中,$∠ACB = 90^{\circ}$,$BC ＞ AC$.以AC和BC为边分别作两个正方形,已知$BD = 5$,$\triangle ABC$的面积是2,求BC的长.

答案： 22.解:
(1)阴影面积等于边长为$(m + n)$的正方形面积减去中间边长为$(m - n)$的正方形面积。阴影面积等于四个长为$m$、宽为$n$的长方形面积之和。$(m + n)^2$，$(m - n)^2$和$mn$之间的数量关系为$(m + n)^2 - (m - n)^2 = 4mn$。左边$=(m + n)^2 - (m - n)^2 = (m + n + m - n)(m + n - m + n) = 4mn$，左边$=$右边，等式成立。
(2)在$Rt\triangle ABC$中，$\angle C = 90^{\circ}$，$S_{\triangle ABC} = \frac{1}{2}AC· BC = 2$，$\therefore AC· BC = 4$，$\because BD = 5$，$\therefore AC + BC = 5$，$(BC - AC)^2 = (BC + AC)^2 - 4BC· AC = 25 - 16 = 9$，$\therefore BC - AC = 3$，可得方程组$\begin{cases}BC - AC = 3\\BC + AC = 5\end{cases}$，解得$\begin{cases}BC = 4\\AC = 1\end{cases}$，即$BC$的长为$4$。