《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

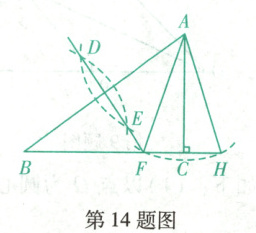
14. (铁岭西丰期末)如图,在$\triangle A B C$中,$\angle A C B=90^{\circ}, A C＜B C$.分别以点$A,B$为圆心,大于$\frac{1}{2} A B$的长为半径作弧,两弧交于$D,E$两点,直线$D E$交$B C$于点$F$,连接$A F$.以点$A$为圆心,$A F$为半径作弧,交$B C$的延长线于点$H$,连接$A H$.若$B C=3$,则$\triangle A F H$的周长为6.

答案： 14.6 【解析】由基本作图方法得出$DE$垂直平分$AB$，则$AF = BF$，$AF = AH$，$AC \perp FH$，$\therefore FC = CH$，$\because AF + FC = BF + FC = AH + CH = BC = 3$，$\therefore \triangle AFH$的周长为$AF + FC + CH + AH = 2BC = 6$.

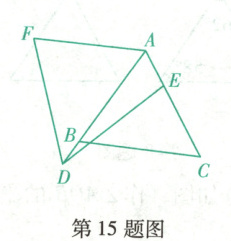
15. (大连高新期末)如图,$\triangle A B C$是等边三角形,边长为8,点$D$在$A B$的延长线上,且$B D=2$,动点$E$从点$A$出发,沿射线$A C$运动,连接$D E$,将线段$D E$绕点$D$按逆时针方向旋转$60^{\circ}$得到线段$D F$,连接$A F$.当$C E=\frac{1}{2} A C$时,则线段$A F$的长为6或2.

答案：
15.6或2 【解析】分两种情况：①当点$E$在线段$AC$上时，过点$D$作$DG // BC$交$AC$的延长线于点$G$，如答图1，$\because \triangle ABC$是等边三角形，$\therefore \angle ABC = \angle ACB = 60^{\circ}$，$\because DG // BC$，$\therefore \angle ADG = \angle ABC = 60^{\circ}$，$\angle G = \angle ACB = 60^{\circ}$，$\therefore \triangle ADG$是等边三角形，$\therefore DG = AD$，由旋转的性质知$DE = DF$，$\angle EDF = 60^{\circ}$，$\therefore \angle EDG = \angle FDA$，$\therefore \triangle EDG \cong \triangle FDA(SAS)$，$\therefore GE = AF$，$\because AB = 8$，$BD = 2$，$\therefore AD = 10$，$\therefore AG = 10$，$\because CE = \frac{1}{2}AC = 4$，$\therefore AE = AC - CE = 8 - 4 = 4$，$\therefore GE = AG - AE = 10 - 4 = 6$，$\therefore AF = 6$；②当点$E$在$AC$的延长线上时，过点$D$作$DH // BC$交$CE$于点$H$，如答图2，同理可得$\triangle EDH \cong \triangle FDA(SAS)$，$\therefore HE = AF$，$\because AE = 8 + 4 = 12$，$AH = AD = 8 + 2 = 10$，$\therefore HE = AE - AH = 12 - 10 = 2$，$\therefore AF = 2$. 综上所述，线段$AF$的长为6或2.
　　　　　　　　 　　　　

16. (每小题5分,共10分)(营口鲅鱼圈期末)
计算:
(1)$8 a^{6} ÷ 2 a^{2}-2 a^{3} · 3 a-\left(3 a^{2}\right)^{2}$;
(2)$3 x(2 x+3)-(2 x-1)(2 x+1)$.

答案： $(1)$计算$8a^{6}÷2a^{2}-2a^{3}·3a-(3a^{2})^{2}$
解：
根据单项式除法法则$a^m÷ a^n = a^{m - n}$，单项式乘法法则$a^m· a^n = a^{m + n}$以及积的乘方法则$(ab)^n=a^nb^n$来计算：
计算$8a^{6}÷2a^{2}$：
根据单项式除法法则$8a^{6}÷2a^{2}=(8÷2)a^{6 - 2}=4a^{4}$。
计算$2a^{3}·3a$：
根据单项式乘法法则$2a^{3}·3a=(2×3)a^{3 + 1}=6a^{4}$。
计算$(3a^{2})^{2}$：
根据积的乘方法则$(3a^{2})^{2}=3^{2}·(a^{2})^{2}=9a^{4}$。
将上述结果代入原式可得：
$8a^{6}÷2a^{2}-2a^{3}·3a-(3a^{2})^{2}=4a^{4}-6a^{4}-9a^{4}$
再根据合并同类项法则$a^m\pm a^m=(1\pm1)a^m$，可得$4a^{4}-6a^{4}-9a^{4}=(4 - 6 - 9)a^{4}=-11a^{4}$。
$(2)$计算$3x(2x + 3)-(2x - 1)(2x + 1)$
解：
计算$3x(2x + 3)$：
根据单项式乘多项式法则$a(b + c)=ab+ac$，可得$3x(2x + 3)=3x·2x+3x·3 = 6x^{2}+9x$。
计算$(2x - 1)(2x + 1)$：
根据平方差公式$(a - b)(a + b)=a^{2}-b^{2}$，这里$a = 2x$，$b = 1$，则$(2x - 1)(2x + 1)=(2x)^{2}-1^{2}=4x^{2}-1$。
将上述结果代入原式可得：
$3x(2x + 3)-(2x - 1)(2x + 1)=6x^{2}+9x-(4x^{2}-1)$
去括号得$6x^{2}+9x - 4x^{2}+1$，再合并同类项$(6x^{2}-4x^{2})+9x + 1=2x^{2}+9x + 1$。
综上，$(1)$的结果为$-11a^{4}$；$(2)$的结果为$2x^{2}+9x + 1$。

17. (8分)(大连庄河期末)
先化简,再求值:$\frac{a}{a^{2}+2 a+1} ÷\left(1-\frac{a}{a+1}\right)$,其中$a=2$.

答案： 解：
$\begin{aligned}&\frac{a}{a^{2}+2a + 1}÷(1 - \frac{a}{a + 1})\\=&\frac{a}{(a + 1)^{2}}÷(\frac{a + 1}{a + 1}-\frac{a}{a + 1})\\=&\frac{a}{(a + 1)^{2}}÷\frac{a + 1 - a}{a + 1}\\=&\frac{a}{(a + 1)^{2}}÷\frac{1}{a + 1}\\=&\frac{a}{(a + 1)^{2}}×(a + 1)\\=&\frac{a}{a + 1}\end{aligned}$
当$a = 2$时，$\frac{a}{a + 1}=\frac{2}{2 + 1}=\frac{2}{3}$。
综上，化简结果为$\frac{a}{a + 1}$，值为$\frac{2}{3}$。