2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. 如图,将一张三角形纸片ABC的一角折叠,使点A落在点$A'$处,折痕为DE.如果$∠A = \alpha$,$∠CDA' = \beta$,$∠BEA' = \gamma$,那么下列式子正确的是(

A.$\gamma = 2\alpha + \beta$
B.$\gamma = \alpha + 2\beta$
C.$\gamma = \alpha + \beta$
D.$\gamma = 180^{\circ} - \alpha - \beta$
A
)
A.$\gamma = 2\alpha + \beta$
B.$\gamma = \alpha + 2\beta$
C.$\gamma = \alpha + \beta$
D.$\gamma = 180^{\circ} - \alpha - \beta$
答案:
8.A [解析]由折叠的性质可知$\angle A=\angle A'=\alpha$,$\angle AED=\angle A'ED=\frac{1}{2}\angle AEA'$,$\because \angle BEA'=\gamma$,$\therefore \angle AEA'=180^{\circ}-\gamma$,$\because \angle AFE=\angle A'+\angle CDA'=\alpha+\beta$,在$\triangle AEF$中,$\angle AEA'+\angle A+\angle AFE=180^{\circ}$,即$180^{\circ}-\gamma+\alpha+(\alpha+\beta)=180^{\circ}$,$\therefore \gamma=2\alpha+\beta$。
9. (营口期末)如图,在$Rt\triangle ABC$中,$∠ABC = 90^{\circ}$,根据尺规作图的痕迹判断,以下结论
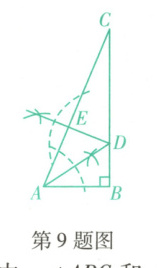
A.$DB = DE$
B.$AB = AE$
C.$∠EDC = ∠BAC$
D.$∠DAC = ∠C$
错
误
的是(D
)
A.$DB = DE$
B.$AB = AE$
C.$∠EDC = ∠BAC$
D.$∠DAC = ∠C$
答案:
9.D
10. (抚顺清原期末)如图,在$\triangle ABC$中,$∠ABC$和$∠ACB$的平分线相交于点O,过点O作$EF // BC$交AB于点E,交AC于点F,过点O作$OD \perp AC$于点D.有下列结论:①$EF = BE + CF$;②$∠BOC = 90^{\circ} + ∠A$;③点O到$\triangle ABC$各边的距离都相等;④设$OD = m$,$AE + AF = n$,则$S_{\triangle AEF} = mn$.其中正确结论的个数是(

A.1
B.2
C.3
D.4
B
)
A.1
B.2
C.3
D.4
答案:
10.B [解析]$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore \angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$,$\angle A+\angle ABC+\angle ACB=180^{\circ}$,$\therefore \angle OBC+\angle OCB=90^{\circ}-\frac{1}{2}\angle A$,$\therefore \angle BOC=180^{\circ}-(\angle OBC+\angle OCB)=90^{\circ}+\frac{1}{2}\angle A$,故②错误;$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore \angle OBC=\angle OBE$,$\angle OCB=\angle OCF$,$\because EF// BC$,$\therefore \angle OBC=\angle EOB$,$\angle OCB=\angle FOC$,$\therefore \angle EOB=\angle OBE$,$\angle FOC=\angle OCF$,$\therefore BE=OE$,$CF=OF$,$\therefore EF=OE+OF=BE+CF$,故①正确;过点$O$作$OM\perp AB$于点$M$,作$ON\perp BC$于点$N$,连接$OA$,如答图,$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore ON=OD=OM=m$,$\therefore S_{\triangle AEF}=S_{\triangle AOE}+S_{\triangle AOF}=\frac{1}{2}AE· OM+\frac{1}{2}AF· OD=\frac{1}{2}m(AE+AF)$,故④错误;$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore$点$O$到$\triangle ABC$各边的距离相等,故③正确。综上所述,正确的结论有①③,共2个。

10.B [解析]$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore \angle OBC=\frac{1}{2}\angle ABC$,$\angle OCB=\frac{1}{2}\angle ACB$,$\angle A+\angle ABC+\angle ACB=180^{\circ}$,$\therefore \angle OBC+\angle OCB=90^{\circ}-\frac{1}{2}\angle A$,$\therefore \angle BOC=180^{\circ}-(\angle OBC+\angle OCB)=90^{\circ}+\frac{1}{2}\angle A$,故②错误;$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore \angle OBC=\angle OBE$,$\angle OCB=\angle OCF$,$\because EF// BC$,$\therefore \angle OBC=\angle EOB$,$\angle OCB=\angle FOC$,$\therefore \angle EOB=\angle OBE$,$\angle FOC=\angle OCF$,$\therefore BE=OE$,$CF=OF$,$\therefore EF=OE+OF=BE+CF$,故①正确;过点$O$作$OM\perp AB$于点$M$,作$ON\perp BC$于点$N$,连接$OA$,如答图,$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore ON=OD=OM=m$,$\therefore S_{\triangle AEF}=S_{\triangle AOE}+S_{\triangle AOF}=\frac{1}{2}AE· OM+\frac{1}{2}AF· OD=\frac{1}{2}m(AE+AF)$,故④错误;$\because$在$\triangle ABC$中,$\angle ABC$和$\angle ACB$的平分线相交于点$O$,$\therefore$点$O$到$\triangle ABC$各边的距离相等,故③正确。综上所述,正确的结论有①③,共2个。

11. 计算$(-2)^{2026}×(\frac{1}{2})^{2027} = $
\frac{1}{2}
.
答案:
11.$\frac{1}{2}$
12. (大连高新期末)定义新运算:$a \oplus b = \frac{1}{a} + \frac{1}{b}$.若$a \oplus (-b) = 3$,则$\frac{3ab}{2a - 2b}$的值是
-\frac{1}{2}
.
答案:
12.$-\frac{1}{2}$
13. (铁岭县期末)点$A(a,3)$,点$B(2,b)$关于y轴对称,则$a + b = $
1
.
答案:
13.1
14. (营口鲅鱼圈期末)如图,在$Rt\triangle ABC$中,$∠C = 90^{\circ}$,$∠BAC$的平分线AD交BC于点D,$CD = 5$,$AB = 6$,则$\triangle ABD$的面积是
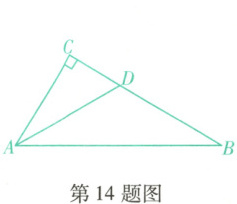
15
.
答案:
14.15 [解析]如答图,过点$D$作$DE\perp AB$于点$E$,
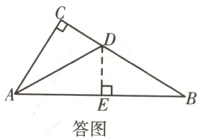
$\because \angle C=90^{\circ}$,$DE\perp AB$,$\angle BAC$的平分线$AD$交$BC$于点$D$,$\therefore DE=CD=5$,$\because AB=6$,$\therefore S_{\triangle ABD}=\frac{1}{2}AB· DE=\frac{1}{2}×5×6=15$。
14.15 [解析]如答图,过点$D$作$DE\perp AB$于点$E$,

$\because \angle C=90^{\circ}$,$DE\perp AB$,$\angle BAC$的平分线$AD$交$BC$于点$D$,$\therefore DE=CD=5$,$\because AB=6$,$\therefore S_{\triangle ABD}=\frac{1}{2}AB· DE=\frac{1}{2}×5×6=15$。
15. (抚顺新宾期末)如图,在四边形ABCD中,$∠C = 50^{\circ}$,$∠B = ∠D = 90^{\circ}$,E,F分别为BC,DC上的点.当$\triangle AEF$的周长最小时,$∠EAF$的度数为
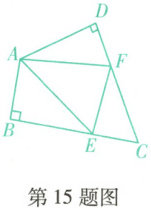
80°
.
答案:
15.$80^{\circ}$ [解析]作点$A$关于$BC$和$CD$的对称点$A'$,$A''$,连接$A'A''$,交$BC$于点$E$,交$CD$于点$F$,则$A'A''$的长即为$\triangle AEF$的周长最小值,作$DA$的延长线$AH$,如答图,$\because \angle C=50^{\circ}$,$\therefore \angle DAB=130^{\circ}$,$\therefore \angle HAA'=50^{\circ}$,$\therefore \angle A'+\angle A''=\angle HAA'=50^{\circ}$,$\because \angle A'=\angle EAA'$,$\angle FAD=\angle A''$,$\therefore \angle EAA'+\angle FAD=50^{\circ}$,$\therefore \angle EAF=130^{\circ}-50^{\circ}=80^{\circ}$。

15.$80^{\circ}$ [解析]作点$A$关于$BC$和$CD$的对称点$A'$,$A''$,连接$A'A''$,交$BC$于点$E$,交$CD$于点$F$,则$A'A''$的长即为$\triangle AEF$的周长最小值,作$DA$的延长线$AH$,如答图,$\because \angle C=50^{\circ}$,$\therefore \angle DAB=130^{\circ}$,$\therefore \angle HAA'=50^{\circ}$,$\therefore \angle A'+\angle A''=\angle HAA'=50^{\circ}$,$\because \angle A'=\angle EAA'$,$\angle FAD=\angle A''$,$\therefore \angle EAA'+\angle FAD=50^{\circ}$,$\therefore \angle EAF=130^{\circ}-50^{\circ}=80^{\circ}$。

查看更多完整答案,请扫码查看


