《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

23. (13分)(葫芦岛期末,有改编)
【问题初探】
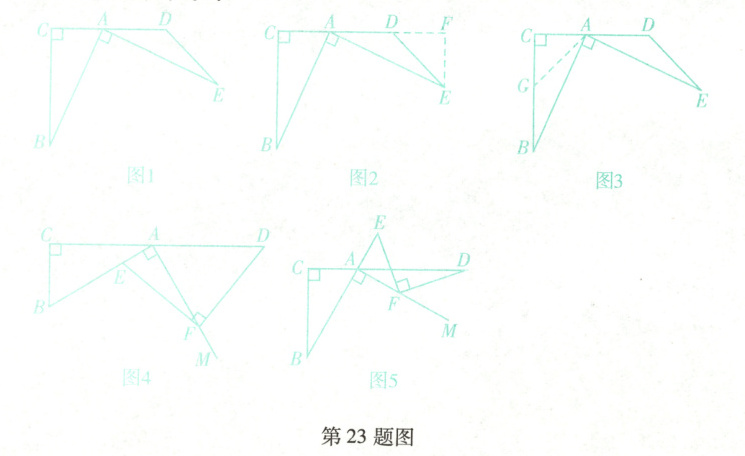
在数学活动课上,李老师给出如下问题:如图1,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,$AE\perp AB$且$AE=AB$,点$D$在$CA$的延长线上,连接$DE$,$\angle ADE=135^{\circ}$,求证:$BC=DC$.
方法一:如图2,小明同学从条件出发,给出如下解题思路:过点$E$作$EF\perp AD$交$AD$的延长线于点$F$,则$\angle EDF=45^{\circ}$,$\triangle EDF$是等腰直角三角形,$EF=DF$,再证明两个三角形全等,转化等量线段.
方法二:如图3,小亮同学从结论出发,给出如下解题思路:在线段$CB$上截取$CG=AC$,则$\triangle ACG$是等腰直角三角形,得到$\angle AGB=135^{\circ}$,再证明两个三角形全等,转化等量线段.
(1)请你选择方法一(填“一”或“二”),并完成证明.
【深入分析】
李老师发现之前两名同学都运用了转化思想,构造全等转化等量线段.为了帮助同学们更好地感悟转化思想,李老师将图1进行变换,提出下面问题,请你解答.
(2)如图4,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,延长$CA$至点$D$,使$AD=AB$,射线$AM\perp AB$,点$E$在线段$AB$上,点$F$在射线$AM$上,连接$EF$,$DF$,$EF=DF$且$EF\perp DF$,求证:$AF=AE+BC$.
【类比推广】
(3)如图5,在$Rt\triangle ABC$中,$\angle C=90^{\circ}$,延长$CA$至点$D$,使$AD=AB$,射线$AM\perp AB$,点$E$在线段$BA$的延长线上,点$F$在射线$AM$上,连接$EF$,$DF$,$EF=DF$且$EF\perp DF$.若$BC=7$,$AE=2$,请直接

写

出

$S_{\triangle ADF}$的大小.

答案：
23.
(1)解:方法一，
∵EF⊥AD，
∴∠F = 90°，
∵∠ADE = 135°，
∴∠EDF = 180° - ∠ADE = 45°，∠DEF = ∠ADE - ∠F = 45°，
∴∠ADF = ∠DEF，
∴DF = EF，
∵∠C = ∠F = 90°，
∴∠B + ∠BAC = 90°，
∵AE⊥AB，
∴∠BAE = 90°，
∴∠BAC + ∠EAF = 90°，
∴∠B = ∠EAF，
∵AB = AE，
∴△ABC≌△EAF(AAS)，
∴AC = EF = DF，BC = AF，
∴BC = AD + DF = AD + AC = DC.
方法二，
∵∠C = 90°，
∴∠CAG = ∠AGC = 45°，
∴∠AGB = 180° - ∠AGC = 135°，
∴∠AGB = ∠D = 135°，同理知∠B = ∠DAE，AB = AE，
∴△ABG≌△EAD(AAS)，
∴BG = AD，
∴BG + CG = AD + AC，
∴BC = DC.
(2)证明:如答图1，过点D作DG⊥AF于点G，同理方法一，得△DGF≌△FEA，∠B = ∠DAF，
∴GF = AE，
∵∠C = ∠AGD = 90°，AB = AD，
∴△ABC≌△DAG(AAS)，
∴BC = AG，
∴AF = FG + AG = AE + BC.

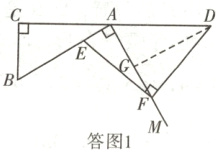
(3)解:如答图2，过点D作DG⊥AM于点G，同理方法一，得△ABC≌△DAG，△DFG≌△FEA，
∴AG = BC = 5，FG = AE = 2，DG = AF = AG - FG = 3，
∴$S_{△ADF}$ = $\frac{1}{2}$AF·DG = $\frac{1}{2}$×3×3 = $\frac{9}{2}$.