2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
8. (抚顺县期末)如图,在$ \triangle ABC $中,$ AB = AC $,$ D $是$ BC $的中点,下列结论
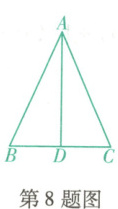
A.$ AD\perp BC $
B.$ \angle B = \angle C $
C.$ AB = 2BD $
D.$ AD $平分$ \angle BAC $
不
正
确
的是(C
)
A.$ AD\perp BC $
B.$ \angle B = \angle C $
C.$ AB = 2BD $
D.$ AD $平分$ \angle BAC $
答案:
8.C
9. (抚顺新宾期末)如图,把$ \triangle ABC $沿$ EF $翻折,叠合后的图形如图,若$ \angle A = 60^{\circ} $,$ \angle 1 = 95^{\circ} $,则$ \angle 2 $的度数是(
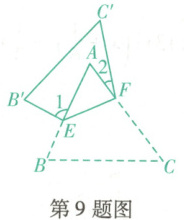
A.$ 15^{\circ} $
B.$ 20^{\circ} $
C.$ 25^{\circ} $
D.$ 35^{\circ} $
C
)
A.$ 15^{\circ} $
B.$ 20^{\circ} $
C.$ 25^{\circ} $
D.$ 35^{\circ} $
答案:
9.C [解析]由折叠的性质知∠BEF=∠B'EF,∠CFE=∠C'FE,
∴180°−∠AEF=∠1+∠AEF,180°−∠AFE=∠2+∠AFE,
∵∠1=95°,
∴∠AEF=$\frac{1}{2}$(180°−95°)=42.5°,
∵∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°−60°−42.5°=77.5°,
∴180°−77.5°=∠2+77.5°,
∴∠2=25°.
∴180°−∠AEF=∠1+∠AEF,180°−∠AFE=∠2+∠AFE,
∵∠1=95°,
∴∠AEF=$\frac{1}{2}$(180°−95°)=42.5°,
∵∠A+∠AEF+∠AFE=180°,
∴∠AFE=180°−60°−42.5°=77.5°,
∴180°−77.5°=∠2+77.5°,
∴∠2=25°.
10. (大连庄河期末)如图,已知在$ \triangle ABC $中,边$ BC $的垂直平分线$ DF $交$ AC $于点$ E $,再以点$ B $为圆心,任意长为半径作弧,交$ BA $,$ BC $于点$ M $,$ N $,再分别以$ M $,$ N $为圆心,大于$ \frac{1}{2}MN $的长为半径作弧交于点$ P $,作射线$ BP $恰好交$ AC $于点$ E $. 若$ AB = 8 $,$ BC = 12 $,$ \triangle BDE $的面积为$ 9 $,则$ \triangle ABC $的面积为(
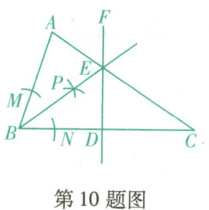
A.$ 9 $
B.$ 12 $
C.$ 30 $
D.$ 27 $
C
)
A.$ 9 $
B.$ 12 $
C.$ 30 $
D.$ 27 $
答案:
10.C [解析]过点E作EG⊥AB于点G,如答图,由作图可知射线BP为∠ABC的平分线,
∴DE=EG,
∵直线DF为线段BC的垂直平分线,
∴∠BDF=90°,BD=CD=$\frac{1}{2}$BC=6,
∵△BDE的面积为9,
∴S△BCE=2S△BDE=18,$\frac{1}{2}$BD·DE=$\frac{1}{2}$×6DE=9,解得DE=3,
∴EG=3,
∴S△ABE=$\frac{1}{2}$AB·EG=$\frac{1}{2}$×8×3=12,
∴S△ABC=S△ABE+S△BCE=12+18=30.

10.C [解析]过点E作EG⊥AB于点G,如答图,由作图可知射线BP为∠ABC的平分线,
∴DE=EG,
∵直线DF为线段BC的垂直平分线,
∴∠BDF=90°,BD=CD=$\frac{1}{2}$BC=6,
∵△BDE的面积为9,
∴S△BCE=2S△BDE=18,$\frac{1}{2}$BD·DE=$\frac{1}{2}$×6DE=9,解得DE=3,
∴EG=3,
∴S△ABE=$\frac{1}{2}$AB·EG=$\frac{1}{2}$×8×3=12,
∴S△ABC=S△ABE+S△BCE=12+18=30.

11. (盘锦兴隆台期末)因式分解:$ a^{3}-ab^{2}= $
a(a+b)(a−b)
.
答案:
11.a(a+b)(a−b)
12. (大连高新期末)“夜深知雪重,时闻折竹声.”这是白居易《夜雪》中对雪的描写. 单个雪花的重量其实很轻,只有$ 0.00003kg $左右,$ 0.00003 $用科学记数法可表示为
3×10−5
.
答案:
12.3×10−5
13. (葫芦岛龙港期末)已知$ 5m^{2}+4m - 1 = 0 $,则代数式$ (2m + 1)^{2}+(m + 3)(m - 3) $的值为
−7
.
答案:
13.−7
14. (抚顺新宾期末)如图,$ AC $平分$ \angle DCB $,$ CB = CD $,$ DA $的延长线交$ BC $于点$ E $. 如果$ \angle EAC = 48^{\circ} $,则$ \angle BAE $的度数为
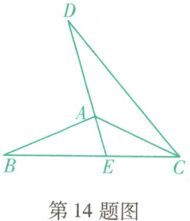
84°
.
答案:
14.84° [解析]
∵AC平分∠DCB,
∴∠BCA=∠DCA,在△ABC和△ADC中,{CB=CD,∠BCA=∠DCA,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=48°,
∴∠B+∠ACB=48°,
∴∠BAE=180°−∠B−∠ACB−∠EAC=180°−48°−48°=84°.
∵AC平分∠DCB,
∴∠BCA=∠DCA,在△ABC和△ADC中,{CB=CD,∠BCA=∠DCA,AC=AC,
∴△ABC≌△ADC(SAS),
∴∠B=∠D,
∴∠B+∠ACB=∠D+∠ACD,
∵∠CAE=∠D+∠ACD=48°,
∴∠B+∠ACB=48°,
∴∠BAE=180°−∠B−∠ACB−∠EAC=180°−48°−48°=84°.
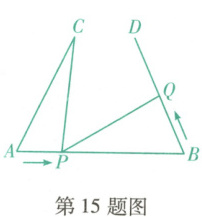
15. (抚顺望花期末)如图,$ AB = 8cm $,$ AC = BD = 6cm $,$ \angle CAB = \angle DBA $,点$ P $在线段$ AB $上以$ 2cm/s $的速度由点$ A $向点$ B $运动,同时,点$ Q $在线段$ BD $上由点$ B $向点$ D $运动,它们运动的时间为$ t(s) $. 设点$ Q $的运动速度为$ xcm/s $,若使得$ \triangle ACP $与$ \triangle BPQ $全等,则$ x $的值为
2或4
$ cm/s $.
答案:
15.2或4 [解析]根据题意可得AP=2t,BP=8−2t,BQ=xt.分两种情况:①当△ACP≌△BPQ时,
∴AC=BP,AP=BQ,即8−2t=6,2t=xt,解得t=1,x=2;②当△ACP≌△BQP时,
∴AP=BP=3,BQ=AC,即2t=3,解得t=$\frac{3}{2}$,
∴BQ=xt=$\frac{3}{2}$x=6,解得x=4.综上所述,x的值为2或4.
∴AC=BP,AP=BQ,即8−2t=6,2t=xt,解得t=1,x=2;②当△ACP≌△BQP时,
∴AP=BP=3,BQ=AC,即2t=3,解得t=$\frac{3}{2}$,
∴BQ=xt=$\frac{3}{2}$x=6,解得x=4.综上所述,x的值为2或4.
查看更多完整答案,请扫码查看


