《2025年1加1轻巧夺冠完美期末八年级数学上册人教版辽宁专版》

23. (13分)(抚顺东洲期末,有改编)
【阅读理解】
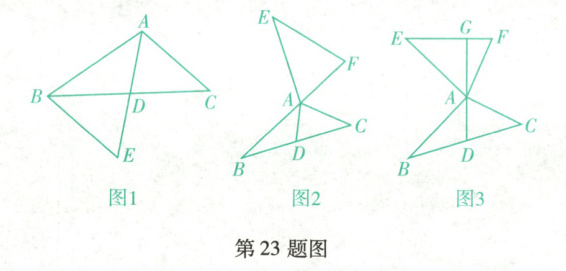
如图1,在$\triangle ABC$中,若$AB = 10$,$AC = 8$,求边BC上的中线AD的取值范围.小明在组内经过合作交流,得到了如下的解决方法:延长AD到点E,使$DE = AD$.请根据小明的方法思考:
(1)证明:$\triangle ADC \cong \triangle EDB$.
(2)连接BE,利用三角形的三边关系求AE的取值范围.
【方法总结】
解题时,条件中若出现"中点""中线"字样,可以考虑延长中线构造全等三角形,把分散的已知条件和所求证的结论集合到同一个三角形中.
【问题解决】
(3)如图2,AD是$\triangle ABC$的中线,$AB = AE$,$AC = AF$,$∠BAE + ∠CAF = 180^{\circ}$,试判断线段EF与AD的数量关系,并说明理由.
(4)在(3)的条件下,若$∠BAE = ∠CAF = 90^{\circ}$,延长DA交EF于点G,如图3,$AD = 2$,$AG = 3$,请

直

接

写

出

$\triangle ABC$的面积.

答案：
23.解:
(1)证明：$\because AD$是中线，$\therefore BD = CD$，又$\because \angle ADC = \angle EDB$，$\therefore \triangle ADC \cong \triangle EDB(SAS)$。
(2)$\because \triangle ADC \cong \triangle EDB$，$\therefore AC = EB = 8$，在$\triangle ABE$中，$AB - EB \lt AE \lt AB + EB$，$\therefore 2 \lt AE \lt 18$，即$2 \lt 2AD \lt 18$，$\therefore 1 \lt AD \lt 9$。
(3)$EF = 2AD$，理由如下：延长$AD$到点$M$，使得$MD = AD$，连接$MB$，如答图$1$，$\therefore AM = AD + MD = 2AD$，$\because AD$是$\triangle ABC$的中线，$\therefore BD = CD$，在$\triangle BDM$和$\triangle CDA$中，$\begin{cases}BD = CD\\\angle BDM = \angle CDA\\MD = AD\end{cases}$，$\therefore \triangle BDM \cong \triangle CDA(SAS)$，$\therefore MB = AC$，$\because AC = AF$，$\therefore MB = AF$，$\therefore \triangle BDM \cong \triangle CDA$，$\therefore \angle MBD = \angle ACD$，$\therefore MB// AC$，$\because \angle ABM + \angle BAC = 180^{\circ}$，$\therefore \angle BAE + \angle CAF = 180^{\circ}$，$\because \angle BAC + \angle FAE = 360^{\circ} - (\angle BAE + \angle CAF) = 360^{\circ} - 180^{\circ} = 180^{\circ}$，$\therefore \angle ABM = \angle FAE$，在$\triangle ABM$和$\triangle EAF$中，$\begin{cases}AB = EA\\\angle ABM = \angle EAF\\MB = AF\end{cases}$，$\therefore \triangle ABM \cong \triangle EAF(SAS)$，$\therefore AM = EF$，$\because AM = 2AD$，$\therefore EF = 2AD$。
　　　
(4)延长$AD$到点$M$，使得$DM = AD$，连接$MB$，由
(3)可知$\angle BAM = \angle E$，$EF = AM = 2AD = 4$，$\because \angle BAE = \angle CAF = 90^{\circ}$，$\therefore \angle BAM + \angle EAG = 90^{\circ}$，$\therefore \angle E + \angle EAG = 90^{\circ}$，即$\angle AGE = 90^{\circ}$，同理得$\triangle ADC \cong \triangle MDB$，$\triangle ABM \cong \triangle EAF$，$S_{\triangle ABC}=S_{\triangle ABM}=S_{\triangle AEF}=\frac{1}{2}EF· AG=\frac{1}{2}×4×3 = 6$。