2026年学易优高考二轮总复习化学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习化学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第45页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
4. (2025·蚌埠市二模)制备二甲醚(${CH_{3}OCH_{3}}$)的方法之一为:
ⅰ.${CO(g) + 2H_{2}(g)\xlongequal{}CH_{3}OH(g)}$ $\Delta H_{1}=-90.7\ kJ·mol^{-1}$ $K_{1}$;
ⅱ.${2CH_{3}OH(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$ $\Delta H_{2}=-23.5\ kJ·mol^{-1}$ $K_{2}$。
回答下列问题:
(1)反应${4H_{2}(g) + 2CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$的$\Delta H=$
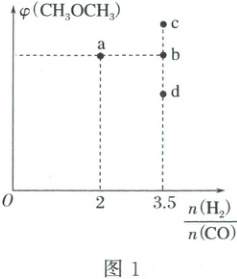
(2)在恒温恒压条件下仅发生反应:${4H_{2}(g) + 2CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$。起始时$H_{2}$、$CO$物质的量之比为$2:1$,${CH_{3}OCH_{3}}$的平衡体积分数$\varphi({CH_{3}OCH_{3}})$对应图1中的a点,若调节起始时$H_{2}$、$CO$物质的量之比为$3.5:1$,则${CH_{3}OCH_{3}}$的平衡体积分数可能对应图1中的______(填“b”“c”或“d”)点。下列不能说明该反应已达到平衡状态的是______(填字母)。
A. $H_{2}$、$CO$、${CH_{3}OCH_{3}}$、${H_{2}O}$的反应速率之比为$4:2:1:1$
B. 混合气体的平均摩尔质量保持不变
C. 容器中气体的密度保持不变
D. 断裂$4$个$H-H$键,同时断裂$2$个$H-O$键
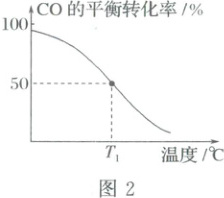
(3)将合成气按$\frac{n(H_{2})}{n(CO)}=1:1$通入密闭反应器中,在压强为$p$的条件下发生反应:${3H_{2}(g) + 3CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + CO_{2}(g)}$,$CO$的平衡转化率随温度的变化关系如图2所示。该反应中反应物的总能量______(填“$<$”或“$>$”)生成物的总能量,温度为$T_{1}$时,$CO_{2}$的平衡分压为______,该温度下,该反应的平衡常数$K_{p}$为______(用平衡分压代替平衡浓度计算,平衡分压$=$总压$×$物质的量分数)。
温馨提示:请做课时精练突破十七$P_{134}$
ⅰ.${CO(g) + 2H_{2}(g)\xlongequal{}CH_{3}OH(g)}$ $\Delta H_{1}=-90.7\ kJ·mol^{-1}$ $K_{1}$;
ⅱ.${2CH_{3}OH(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$ $\Delta H_{2}=-23.5\ kJ·mol^{-1}$ $K_{2}$。
回答下列问题:
(1)反应${4H_{2}(g) + 2CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$的$\Delta H=$
−204.9
$\ kJ·mol^{-1}$,该反应的平衡常数$K=$K₁²·K₂
$$(用$K_{1}$、$K_{2}$表示)。(2)在恒温恒压条件下仅发生反应:${4H_{2}(g) + 2CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + H_{2}O(g)}$。起始时$H_{2}$、$CO$物质的量之比为$2:1$,${CH_{3}OCH_{3}}$的平衡体积分数$\varphi({CH_{3}OCH_{3}})$对应图1中的a点,若调节起始时$H_{2}$、$CO$物质的量之比为$3.5:1$,则${CH_{3}OCH_{3}}$的平衡体积分数可能对应图1中的______(填“b”“c”或“d”)点。下列不能说明该反应已达到平衡状态的是______(填字母)。
A. $H_{2}$、$CO$、${CH_{3}OCH_{3}}$、${H_{2}O}$的反应速率之比为$4:2:1:1$
B. 混合气体的平均摩尔质量保持不变
C. 容器中气体的密度保持不变
D. 断裂$4$个$H-H$键,同时断裂$2$个$H-O$键
(3)将合成气按$\frac{n(H_{2})}{n(CO)}=1:1$通入密闭反应器中,在压强为$p$的条件下发生反应:${3H_{2}(g) + 3CO(g)\xlongequal{}CH_{3}OCH_{3}(g) + CO_{2}(g)}$,$CO$的平衡转化率随温度的变化关系如图2所示。该反应中反应物的总能量______(填“$<$”或“$>$”)生成物的总能量,温度为$T_{1}$时,$CO_{2}$的平衡分压为______,该温度下,该反应的平衡常数$K_{p}$为______(用平衡分压代替平衡浓度计算,平衡分压$=$总压$×$物质的量分数)。
温馨提示:请做课时精练突破十七$P_{134}$


答案:
$(1)−204.9 K_1^2 · K_2$
(2)d A
$(3)> \frac {p}{8} \frac {4096}{729p^4}$
解析:
(1)根据盖斯定律,方程式Ⅰ×2 + Ⅱ可得$4H_2(g) + 2CO(g) \rightleftharpoons CH_3OCH_3(g) + H_2O(g),$故$\Delta H = −90.7 kJ · mol^{-1} × 2 + (−23.5 kJ · mol^{-1}) = −204.9 kJ · mol^{-1},$方程式计量数加倍,则平衡常数变为原来的平方,方程式相加,则平衡常数相乘,该反应的平衡常数$K = K_1^2 · K_2;$
(2)起始时$H_2、$CO物质的量之比为2 : 1,此时等于计量数之比,平衡时产物的体积分数最大,若调节起始时$H_2、$CO物质的量之比为3.5 : 1,恒温恒压条件下,与原平衡相比,相当于减压,平衡逆向移动,再次平衡时$CH_3OCH_3$的平衡体积分数会变小,故d点符合;$H_2、$CO、$CH_3OCH_3、$$H_2O$的反应速率等于计量数之比,始终为4 : 2 : 1 : 1,不能说明达到平衡,故A选;若没有平衡,反应向右进行时,混合气体的平均摩尔质量会增大,现保持不变能说明达到平衡,故B不选;反应在恒温恒压条件发生,反应前后气体的体积变化,则密度是变量,现保持不变能说明达到平衡,故C不选;断裂4个H—H键,同时断裂2个H—O键,说明正逆反应速率相等,能说明反应达到平衡,故D不选;答案选A;
(3)CO的平衡转化率随温度的变化关系如图2所示,即温度升高,CO的平衡转化率降低,表示升高温度平衡逆向移动,该反应为放热反应,反应物的总能量 > 生成物的总能量;合成气按$\frac {n(H_2)}{n(CO)} = 1 : 1$通入密闭反应器中,设$H_2$和CO的物质的量均为3 mol,温度为$T_1$时,CO的平衡转化率为50%,列三段式如下:
$3H_2(g) + 3CO(g) \rightleftharpoons CH_3OCH_3(g) + CO_2(g)$
$\begin{matrix}$
起始(mol) & 3 & 3 & 0 & 0 \\
变化(mol) & 1.5 & 1.5 & 0.5 & 0.5 \\
平衡(mol) & 1.5 & 1.5 & 0.5 & 0.5 \\
$\end{matrix}$
$CO_2$的平衡分压为$p × \frac {0.5}{1.5 + 1.5 + 0.5 + 0.5} = \frac {p}{8},$
同理可得$p(CH_3OCH_3) = \frac {p}{8},$$p(H_2) = p(CO) = \frac {3p}{8},$该反应的平衡常数$K_p = \frac {p(CH_3OCH_3)p(CO_2)}{p^3(H_2)p^3(CO)} = \frac {\frac {p}{8} × \frac {p}{8}}{( \frac {3p}{8} )^3 × ( \frac {3p}{8} )^3} = \frac {4096}{729p^4}。$
(2)d A
$(3)> \frac {p}{8} \frac {4096}{729p^4}$
解析:
(1)根据盖斯定律,方程式Ⅰ×2 + Ⅱ可得$4H_2(g) + 2CO(g) \rightleftharpoons CH_3OCH_3(g) + H_2O(g),$故$\Delta H = −90.7 kJ · mol^{-1} × 2 + (−23.5 kJ · mol^{-1}) = −204.9 kJ · mol^{-1},$方程式计量数加倍,则平衡常数变为原来的平方,方程式相加,则平衡常数相乘,该反应的平衡常数$K = K_1^2 · K_2;$
(2)起始时$H_2、$CO物质的量之比为2 : 1,此时等于计量数之比,平衡时产物的体积分数最大,若调节起始时$H_2、$CO物质的量之比为3.5 : 1,恒温恒压条件下,与原平衡相比,相当于减压,平衡逆向移动,再次平衡时$CH_3OCH_3$的平衡体积分数会变小,故d点符合;$H_2、$CO、$CH_3OCH_3、$$H_2O$的反应速率等于计量数之比,始终为4 : 2 : 1 : 1,不能说明达到平衡,故A选;若没有平衡,反应向右进行时,混合气体的平均摩尔质量会增大,现保持不变能说明达到平衡,故B不选;反应在恒温恒压条件发生,反应前后气体的体积变化,则密度是变量,现保持不变能说明达到平衡,故C不选;断裂4个H—H键,同时断裂2个H—O键,说明正逆反应速率相等,能说明反应达到平衡,故D不选;答案选A;
(3)CO的平衡转化率随温度的变化关系如图2所示,即温度升高,CO的平衡转化率降低,表示升高温度平衡逆向移动,该反应为放热反应,反应物的总能量 > 生成物的总能量;合成气按$\frac {n(H_2)}{n(CO)} = 1 : 1$通入密闭反应器中,设$H_2$和CO的物质的量均为3 mol,温度为$T_1$时,CO的平衡转化率为50%,列三段式如下:
$3H_2(g) + 3CO(g) \rightleftharpoons CH_3OCH_3(g) + CO_2(g)$
$\begin{matrix}$
起始(mol) & 3 & 3 & 0 & 0 \\
变化(mol) & 1.5 & 1.5 & 0.5 & 0.5 \\
平衡(mol) & 1.5 & 1.5 & 0.5 & 0.5 \\
$\end{matrix}$
$CO_2$的平衡分压为$p × \frac {0.5}{1.5 + 1.5 + 0.5 + 0.5} = \frac {p}{8},$
同理可得$p(CH_3OCH_3) = \frac {p}{8},$$p(H_2) = p(CO) = \frac {3p}{8},$该反应的平衡常数$K_p = \frac {p(CH_3OCH_3)p(CO_2)}{p^3(H_2)p^3(CO)} = \frac {\frac {p}{8} × \frac {p}{8}}{( \frac {3p}{8} )^3 × ( \frac {3p}{8} )^3} = \frac {4096}{729p^4}。$
1. (2025·安徽卷)Ⅰ. 通过甲酸分解可获得超高纯度的 CO。甲酸有两种可能的分解反应:
① $ HCOOH(g) \xlongequal{} CO(g) + H_2O(g) $ $ \Delta H_1 = +26.3 \, kJ · mol^{-1} $
② $ HCOOH(g) \xlongequal{} CO_2(g) + H_2(g) $ $ \Delta H_2 = -14.9 \, kJ · mol^{-1} $
(1) 反应 $ CO(g) + H_2O(g) \xlongequal{} CO_2(g) + H_2(g) $ 的 $ \Delta H = $
(2) 一定温度下,向恒容密闭容器中通入一定量的 HCOOH(g),发生上述两个分解反应,下列说法中能表明反应达到平衡状态的是
a. 气体密度不变
b. 气体总压强不变
c. $ H_2O(g) $ 的浓度不变
d. CO 和 $ CO_2 $ 的物质的量相等
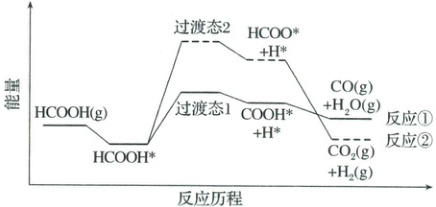
(3) 一定温度下,使用某催化剂时反应历程如图,反应①的选择性接近 100%,原因是 ______;升高温度,反应历程不变,反应①的选择性下降,可能的原因是 ______。
Ⅱ. 甲烷和二氧化碳重整是制取合成气 (CO 和 $ H_2 $) 的重要方法,主要反应有:
③ $ CH_4(g) + CO_2(g) \xlongequal{} 2CO(g) + 2H_2(g) $
④ $ CO_2(g) + H_2(g) \xlongequal{} CO(g) + H_2O(g) $
⑤ $ CH_4(g) + H_2O(g) \xlongequal{} CO(g) + 3H_2(g) $
(4) 恒温恒容条件下,可提高 $ CH_4 $ 平衡转化率的措施有
a. 增加原料中 $ CH_4 $ 的量
b. 增加原料中 $ CO_2 $ 的量
c. 通入 Ar 气
(5) 恒温恒压密闭容器中,投入不同物质的量之比的 $ CH_4/CO_2/Ar $ 混合气,投料组成与 $ CH_4 $ 和 $ CO_2 $ 的平衡转化率之间的关系如图。
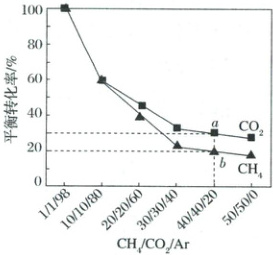
ⅰ. 投料组成中 Ar 含量下降,平衡体系中 $ n(CO) : n(H_2) $ 的值将
ⅱ. 若平衡时 Ar 的分压为 $ p \, kPa $,根据 a、b 两点计算反应⑤的平衡常数 $ K_p = $
① $ HCOOH(g) \xlongequal{} CO(g) + H_2O(g) $ $ \Delta H_1 = +26.3 \, kJ · mol^{-1} $
② $ HCOOH(g) \xlongequal{} CO_2(g) + H_2(g) $ $ \Delta H_2 = -14.9 \, kJ · mol^{-1} $
(1) 反应 $ CO(g) + H_2O(g) \xlongequal{} CO_2(g) + H_2(g) $ 的 $ \Delta H = $
-41.2
$ kJ · mol^{-1} $。(2) 一定温度下,向恒容密闭容器中通入一定量的 HCOOH(g),发生上述两个分解反应,下列说法中能表明反应达到平衡状态的是
bc
(填标号)。a. 气体密度不变
b. 气体总压强不变
c. $ H_2O(g) $ 的浓度不变
d. CO 和 $ CO_2 $ 的物质的量相等
(3) 一定温度下,使用某催化剂时反应历程如图,反应①的选择性接近 100%,原因是 ______;升高温度,反应历程不变,反应①的选择性下降,可能的原因是 ______。

Ⅱ. 甲烷和二氧化碳重整是制取合成气 (CO 和 $ H_2 $) 的重要方法,主要反应有:
③ $ CH_4(g) + CO_2(g) \xlongequal{} 2CO(g) + 2H_2(g) $
④ $ CO_2(g) + H_2(g) \xlongequal{} CO(g) + H_2O(g) $
⑤ $ CH_4(g) + H_2O(g) \xlongequal{} CO(g) + 3H_2(g) $
(4) 恒温恒容条件下,可提高 $ CH_4 $ 平衡转化率的措施有
b
(填标号)。a. 增加原料中 $ CH_4 $ 的量
b. 增加原料中 $ CO_2 $ 的量
c. 通入 Ar 气
(5) 恒温恒压密闭容器中,投入不同物质的量之比的 $ CH_4/CO_2/Ar $ 混合气,投料组成与 $ CH_4 $ 和 $ CO_2 $ 的平衡转化率之间的关系如图。

ⅰ. 投料组成中 Ar 含量下降,平衡体系中 $ n(CO) : n(H_2) $ 的值将
增大
(填“增大”“减小”或“不变”)。ⅱ. 若平衡时 Ar 的分压为 $ p \, kPa $,根据 a、b 两点计算反应⑤的平衡常数 $ K_p = $
$\frac{27}{40}p^2$
$ (kPa)^2 $ (用含 $ p $ 的代数式表示,$ K_p $ 是用分压代替浓度计算的平衡常数,分压 = 总压 × 物质的量分数)。
答案:
1.答案:
(1)-41.2
(2)bc
(3)反应①活化能远小于反应② 升高温度,反应②的反应速率提升程度更大
(4)b
(5)ⅰ.增大ⅱ.$\frac{27}{40}p^2$
解析:
(1)根据盖斯定律,由反应②一反应①,可得$\mathrm{CO(g)+H_2O(g)=CO_2(g)+H_2(g)}\ \Delta H =-14.9\ \mathrm{kJ· mol^{-1}}-26.3\ \mathrm{kJ· mol^{-1}}=-41.2\ \mathrm{kJ· mol^{-1}}$。
(2)该反应中反应物、生成物均为气体,气体总质量不变,容器恒容,则气体密度始终不变,故a错误;反应①和②反应前后气体分子数均不相等,气体总压强为变量,则气体总压强不变可以说明反应达到平衡状态,故b正确;$\mathrm{H_2O(g)}$的浓度不变,则反应体系中各物质浓度均不变,可以说明反应达到平衡状态,故c正确;$\mathrm{CO}$和$\mathrm{CO_2}$的物质的量相等,不能说明各物质浓度不变,不能说明反应达到平衡状态,故d错误。
(3)由图可知,使用该催化剂时反应①的活化能远小于反应②的,故此时反应①的选择性可接近100%;活化能越高的反应的速率对温度越敏感,反应②的活化能更高,升温对其化学反应速率的增加更明显,故升高温度,反应①的选择性下降。
(4)增加原料中$\mathrm{CH_4}$的量,反应③和反应⑤平衡正向移动,但$\mathrm{CH_4}$的平衡转化率降低,故a错误;增加原料中$\mathrm{CO_2}$的量,反应③平衡正向移动,$\mathrm{CH_4}$的平衡转化率增大,故b正确;恒容条件下通入$\mathrm{Ar}$气,体系压强增大,但各反应物浓度不变,平衡不移动,$\mathrm{CH_4}$转化率不变,故c错误。
(5)ⅰ.由题图知,随着投料组成中$\mathrm{Ar}$含量下降,$\mathrm{CO_2}$的平衡转化率大于$\mathrm{CH_4}$的平衡转化率,说明反应④正向进行程度大于反应⑤正向进行程度,故平衡体系中$n(\mathrm{CO})$:$n(\mathrm{H_2})$的值将增大。ⅱ.根据a、b两点起始时$\mathrm{CH_4}/\mathrm{CO_2}/\mathrm{Ar}$的物质的量之比为$40/40/20$,平衡时$\mathrm{CO_2}$转化率为$30\%$,$\mathrm{CH_4}$转化率为$20\%$,设起始时$\mathrm{CH_4}$、$\mathrm{CO_2}$、$\mathrm{Ar}$的物质的量分别为$2\ \mathrm{mol}$、
学易优 高考二轮总复习 化学
$1\ \mathrm{mol}$,反应③中$\mathrm{CH_4}$转化$a\ \mathrm{mol}$,则反应⑤中$\mathrm{CH_4}$转化$(2×20\%-a)\ \mathrm{mol}$,反应④中$\mathrm{CO_2}$转化$(2×30\%-a)\ \mathrm{mol}$,列关系式如下:
③$\mathrm{CH_4(g)+CO_2(g)=2CO(g)+2H_2(g)}$
转化量/mol:$a$ $a$ $2a$ $2a$
④$\mathrm{CO_2(g)+H_2(g)=CO(g)+H_2O(g)}$
转化量/mol:$0.6-a$ $0.6-a$ $0.6-a$ $0.6-a$
⑤$\mathrm{CH_4(g)+H_2O(g)=CO(g)+3H_2(g)}$
转化量/mol:$0.4-a$ $0.4-a$ $0.4-a$ $3(0.4-a)$
平衡时$n(\mathrm{CH_4})=1.6\ \mathrm{mol}$,$n(\mathrm{CO_2})=1.4\ \mathrm{mol}$,
$n(\mathrm{CO})=2a\ \mathrm{mol}+(0.6-a)\ \mathrm{mol}+(0.4-a)\ \mathrm{mol}=1\ \mathrm{mol}$,$n(\mathrm{H_2})=2a\ \mathrm{mol}+3(0.4-a)\ \mathrm{mol}-(0.6-a)\ \mathrm{mol}=0.6\ \mathrm{mol}$,$n(\mathrm{H_2O})=(0.6-a)\ \mathrm{mol}-(0.4-a)\ \mathrm{mol}=0.2\ \mathrm{mol}$。
$n(\mathrm{Ar})=1\ \mathrm{mol}$
另解:根据原子守恒法进行分析。
起始量
$n(\mathrm{CO_2})=2\ \mathrm{mol}×(1 - 30\%)=1.4\ \mathrm{mol}$
$n(\mathrm{CH_4})=2\ \mathrm{mol}×(1 - 20\%)=1.6\ \mathrm{mol}$
$n(\mathrm{Ar})=1\ \mathrm{mol}$
$n(\mathrm{CO_2})=2\ \mathrm{mol}$
$n(\mathrm{CH_4})=2\ \mathrm{mol}$
$n(\mathrm{Ar})=1\ \mathrm{mol}$
根据C守恒:$n(\mathrm{CO})=2\ \mathrm{mol}+2\ \mathrm{mol}-1.4\ \mathrm{mol}-1.6\ \mathrm{mol}=1\ \mathrm{mol}$
根据O守恒:$n(\mathrm{H_2O})=2\ \mathrm{mol}×2-1.4\ \mathrm{mol}×2-1\ \mathrm{mol}=0.2\ \mathrm{mol}$
根据H守恒:$n(\mathrm{H_2})=(2\ \mathrm{mol}×4-1.6\ \mathrm{mol}×4-0.2\ \mathrm{mol}×2)×\frac{1}{2}=0.6\ \mathrm{mol}$
恒压密闭容器中,气体的分压之比等于物质的量之比,平衡时$\mathrm{Ar}$的分压为$p\ \mathrm{kPa}$,则$p(\mathrm{CH_4})=1.6p\ \mathrm{kPa}$,$p(\mathrm{H_2O})=0.2p\ \mathrm{kPa}$,$p(\mathrm{CO})=p\ \mathrm{kPa}$,$p(\mathrm{H_2})=0.6p\ \mathrm{kPa}$,故$K_p=\frac{p(\mathrm{CO})× p^3(\mathrm{H_2})}{p(\mathrm{CH_4})× p(\mathrm{H_2O})}=\frac{p\ \mathrm{kPa}×(0.6p\ \mathrm{kPa})^3}{1.6p\ \mathrm{kPa}×0.2p\ \mathrm{kPa}}=\frac{27p^2}{40}(\mathrm{kPa})^2$。
(1)-41.2
(2)bc
(3)反应①活化能远小于反应② 升高温度,反应②的反应速率提升程度更大
(4)b
(5)ⅰ.增大ⅱ.$\frac{27}{40}p^2$
解析:
(1)根据盖斯定律,由反应②一反应①,可得$\mathrm{CO(g)+H_2O(g)=CO_2(g)+H_2(g)}\ \Delta H =-14.9\ \mathrm{kJ· mol^{-1}}-26.3\ \mathrm{kJ· mol^{-1}}=-41.2\ \mathrm{kJ· mol^{-1}}$。
(2)该反应中反应物、生成物均为气体,气体总质量不变,容器恒容,则气体密度始终不变,故a错误;反应①和②反应前后气体分子数均不相等,气体总压强为变量,则气体总压强不变可以说明反应达到平衡状态,故b正确;$\mathrm{H_2O(g)}$的浓度不变,则反应体系中各物质浓度均不变,可以说明反应达到平衡状态,故c正确;$\mathrm{CO}$和$\mathrm{CO_2}$的物质的量相等,不能说明各物质浓度不变,不能说明反应达到平衡状态,故d错误。
(3)由图可知,使用该催化剂时反应①的活化能远小于反应②的,故此时反应①的选择性可接近100%;活化能越高的反应的速率对温度越敏感,反应②的活化能更高,升温对其化学反应速率的增加更明显,故升高温度,反应①的选择性下降。
(4)增加原料中$\mathrm{CH_4}$的量,反应③和反应⑤平衡正向移动,但$\mathrm{CH_4}$的平衡转化率降低,故a错误;增加原料中$\mathrm{CO_2}$的量,反应③平衡正向移动,$\mathrm{CH_4}$的平衡转化率增大,故b正确;恒容条件下通入$\mathrm{Ar}$气,体系压强增大,但各反应物浓度不变,平衡不移动,$\mathrm{CH_4}$转化率不变,故c错误。
(5)ⅰ.由题图知,随着投料组成中$\mathrm{Ar}$含量下降,$\mathrm{CO_2}$的平衡转化率大于$\mathrm{CH_4}$的平衡转化率,说明反应④正向进行程度大于反应⑤正向进行程度,故平衡体系中$n(\mathrm{CO})$:$n(\mathrm{H_2})$的值将增大。ⅱ.根据a、b两点起始时$\mathrm{CH_4}/\mathrm{CO_2}/\mathrm{Ar}$的物质的量之比为$40/40/20$,平衡时$\mathrm{CO_2}$转化率为$30\%$,$\mathrm{CH_4}$转化率为$20\%$,设起始时$\mathrm{CH_4}$、$\mathrm{CO_2}$、$\mathrm{Ar}$的物质的量分别为$2\ \mathrm{mol}$、
学易优 高考二轮总复习 化学
$1\ \mathrm{mol}$,反应③中$\mathrm{CH_4}$转化$a\ \mathrm{mol}$,则反应⑤中$\mathrm{CH_4}$转化$(2×20\%-a)\ \mathrm{mol}$,反应④中$\mathrm{CO_2}$转化$(2×30\%-a)\ \mathrm{mol}$,列关系式如下:
③$\mathrm{CH_4(g)+CO_2(g)=2CO(g)+2H_2(g)}$
转化量/mol:$a$ $a$ $2a$ $2a$
④$\mathrm{CO_2(g)+H_2(g)=CO(g)+H_2O(g)}$
转化量/mol:$0.6-a$ $0.6-a$ $0.6-a$ $0.6-a$
⑤$\mathrm{CH_4(g)+H_2O(g)=CO(g)+3H_2(g)}$
转化量/mol:$0.4-a$ $0.4-a$ $0.4-a$ $3(0.4-a)$
平衡时$n(\mathrm{CH_4})=1.6\ \mathrm{mol}$,$n(\mathrm{CO_2})=1.4\ \mathrm{mol}$,
$n(\mathrm{CO})=2a\ \mathrm{mol}+(0.6-a)\ \mathrm{mol}+(0.4-a)\ \mathrm{mol}=1\ \mathrm{mol}$,$n(\mathrm{H_2})=2a\ \mathrm{mol}+3(0.4-a)\ \mathrm{mol}-(0.6-a)\ \mathrm{mol}=0.6\ \mathrm{mol}$,$n(\mathrm{H_2O})=(0.6-a)\ \mathrm{mol}-(0.4-a)\ \mathrm{mol}=0.2\ \mathrm{mol}$。
$n(\mathrm{Ar})=1\ \mathrm{mol}$
另解:根据原子守恒法进行分析。
起始量
$n(\mathrm{CO_2})=2\ \mathrm{mol}×(1 - 30\%)=1.4\ \mathrm{mol}$
$n(\mathrm{CH_4})=2\ \mathrm{mol}×(1 - 20\%)=1.6\ \mathrm{mol}$
$n(\mathrm{Ar})=1\ \mathrm{mol}$
$n(\mathrm{CO_2})=2\ \mathrm{mol}$
$n(\mathrm{CH_4})=2\ \mathrm{mol}$
$n(\mathrm{Ar})=1\ \mathrm{mol}$
根据C守恒:$n(\mathrm{CO})=2\ \mathrm{mol}+2\ \mathrm{mol}-1.4\ \mathrm{mol}-1.6\ \mathrm{mol}=1\ \mathrm{mol}$
根据O守恒:$n(\mathrm{H_2O})=2\ \mathrm{mol}×2-1.4\ \mathrm{mol}×2-1\ \mathrm{mol}=0.2\ \mathrm{mol}$
根据H守恒:$n(\mathrm{H_2})=(2\ \mathrm{mol}×4-1.6\ \mathrm{mol}×4-0.2\ \mathrm{mol}×2)×\frac{1}{2}=0.6\ \mathrm{mol}$
恒压密闭容器中,气体的分压之比等于物质的量之比,平衡时$\mathrm{Ar}$的分压为$p\ \mathrm{kPa}$,则$p(\mathrm{CH_4})=1.6p\ \mathrm{kPa}$,$p(\mathrm{H_2O})=0.2p\ \mathrm{kPa}$,$p(\mathrm{CO})=p\ \mathrm{kPa}$,$p(\mathrm{H_2})=0.6p\ \mathrm{kPa}$,故$K_p=\frac{p(\mathrm{CO})× p^3(\mathrm{H_2})}{p(\mathrm{CH_4})× p(\mathrm{H_2O})}=\frac{p\ \mathrm{kPa}×(0.6p\ \mathrm{kPa})^3}{1.6p\ \mathrm{kPa}×0.2p\ \mathrm{kPa}}=\frac{27p^2}{40}(\mathrm{kPa})^2$。
查看更多完整答案,请扫码查看


