2026年学易优高考二轮总复习化学
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年学易优高考二轮总复习化学 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第43页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
2. (2025·河北卷)乙二醇($EG$)是一种重要的基础化工原料,可通过石油化工和煤化工等工业路线合成。
(1)石油化工路线中,环氧乙烷($EO$)水合工艺是一种成熟的乙二醇生产方法,环氧乙烷和水反应生成乙二醇,伴随生成二乙二醇($DEG$)的副反应。
主反应:${EO(aq) + H_{2}O(l)\xlongequal{}EG(aq)}$ $\Delta H<0$
副反应:${EO(aq) + EG(aq)\xlongequal{}DEG(aq)}$
体系中环氧乙烷初始浓度为$1.5\ mol·L^{-1}$,恒温下反应$30\ min$,环氧乙烷完全转化,产物中$n(EG):n(DEG)=10:1$。
①$0\sim30\ min$内,$v_{总}(EO)=$
②下列说法正确的是
a. 主反应中,生成物总能量高于反应物总能量
b. $0\sim30\ min$内,$v_{总}(EO)=v_{总}(EG)$
c. $0\sim30\ min$内,$v_{主}(EG):v_{副}(DEG)=11:1$
d. 选择适当催化剂可提高乙二醇的最终产率
(2)煤化工路线中,利用合成气直接合成乙二醇,原子利用率可达$100\%$,具有广阔的发展前景。反应如下:
${2CO(g) + 3H_{2}(g)\xlongequal{}HOCH_{2}CH_{2}OH(g)}$ $\Delta H$
按化学计量比进料,固定平衡转化率$\alpha$,探究温度与压强的关系。$\alpha$分别为$0.4$、$0.5$和$0.6$时,温度与压强的关系如图:
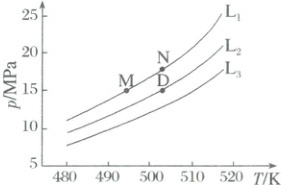
①代表$\alpha = 0.6$的曲线为______(填“$L_{1}$”“$L_{2}$”或“$L_{3}$”);原因是______。
②$\Delta H$
③已知:反应$a{A(g) + bB(g)\xlongequal{}yY(g) + zZ(g)}$,$K_{x}=\frac{x^{y}(Y)x^{z}(Z)}{x^{a}(A)x^{b}(B)}$,$x$为组分的物质的量分数。
$M$、$N$两点对应的体系,$K_{x}(M)$
④已知:反应$a{A(g) + bB(g)\xlongequal{}yY(g) + zZ(g)}$,$K_{p}=\frac{p^{y}(Y)p^{z}(Z)}{p^{a}(A)p^{b}(B)}$,$p$为组分的分压。调整进料比为$n(CO):n(H_{2})=m:3$,系统压强维持$p_{0}\ MPa$,使$\alpha(H_{2}) = 0.75$,此时$K_{p}=$_________$\ MPa^{-4}$(用含有$m$和$p_{0}$的代数式表示)。
(1)石油化工路线中,环氧乙烷($EO$)水合工艺是一种成熟的乙二醇生产方法,环氧乙烷和水反应生成乙二醇,伴随生成二乙二醇($DEG$)的副反应。
主反应:${EO(aq) + H_{2}O(l)\xlongequal{}EG(aq)}$ $\Delta H<0$
副反应:${EO(aq) + EG(aq)\xlongequal{}DEG(aq)}$
体系中环氧乙烷初始浓度为$1.5\ mol·L^{-1}$,恒温下反应$30\ min$,环氧乙烷完全转化,产物中$n(EG):n(DEG)=10:1$。
①$0\sim30\ min$内,$v_{总}(EO)=$
0.05
$\ mol·L^{-1}·min^{-1}$。②下列说法正确的是
cd
(填序号)。a. 主反应中,生成物总能量高于反应物总能量
b. $0\sim30\ min$内,$v_{总}(EO)=v_{总}(EG)$
c. $0\sim30\ min$内,$v_{主}(EG):v_{副}(DEG)=11:1$
d. 选择适当催化剂可提高乙二醇的最终产率
(2)煤化工路线中,利用合成气直接合成乙二醇,原子利用率可达$100\%$,具有广阔的发展前景。反应如下:
${2CO(g) + 3H_{2}(g)\xlongequal{}HOCH_{2}CH_{2}OH(g)}$ $\Delta H$
按化学计量比进料,固定平衡转化率$\alpha$,探究温度与压强的关系。$\alpha$分别为$0.4$、$0.5$和$0.6$时,温度与压强的关系如图:

①代表$\alpha = 0.6$的曲线为______(填“$L_{1}$”“$L_{2}$”或“$L_{3}$”);原因是______。
②$\Delta H$
<
$0$(填“$>$”“$<$”或“$=$”)。③已知:反应$a{A(g) + bB(g)\xlongequal{}yY(g) + zZ(g)}$,$K_{x}=\frac{x^{y}(Y)x^{z}(Z)}{x^{a}(A)x^{b}(B)}$,$x$为组分的物质的量分数。
$M$、$N$两点对应的体系,$K_{x}(M)$
=
$K_{x}(N)$(填“$>$”“$<$”或“$=$”),$D$点对应体系的$K_{x}$的值为12
。④已知:反应$a{A(g) + bB(g)\xlongequal{}yY(g) + zZ(g)}$,$K_{p}=\frac{p^{y}(Y)p^{z}(Z)}{p^{a}(A)p^{b}(B)}$,$p$为组分的分压。调整进料比为$n(CO):n(H_{2})=m:3$,系统压强维持$p_{0}\ MPa$,使$\alpha(H_{2}) = 0.75$,此时$K_{p}=$_________$\ MPa^{-4}$(用含有$m$和$p_{0}$的代数式表示)。
答案:
(1)①0.05 ②cd
$(2)①L_1 $该反应为气体分子数减小的反应,温度相同时,增大压强,平衡正向移动,固定平衡转化率增大 ②< ③= 12
$ ④\frac {(m - 1.5)^2}{m p_o} × ( \frac {0.75}{m p_o} )^2$
解析:
(1)①环氧乙烷的初始浓度为$1.5 mol · L^{-1},$反应30 min,环氧乙烷完全转化,则0∼30 min内,v_总$(EO) = \frac {\Delta c_总(EO)}{\Delta t} = \frac {1.5 mol · L^{-1}}{30 min} = 0.05 mol · L^{-1} · min^{-1}。$②主反应$\Delta H $< 0,为放热反应,生成物总能量低于反应物总能量,a错误;由题目信息知,合成乙二醇的过程中伴随着副反应的发生,EG既是主反应的生成物,又是副反应的反应物,即EG的浓度变化量小于EO的浓度变化量,故v_总(EO) > v_总(EG),b错误;由题目信息知,反应完成后产物中n(EG) : n(DEG) = 10 : 1,即$\Delta n(EG) : \Delta n(DEG) = 10 : 1,$反应时间相同,则v_总(EG) : v_制(DEG) = 10 : 1,结合v_总(EG) = v_主(EG) - v_制(EG)可得,$\frac {v_主(EG) - v_制(EG)}{v_制(DEG)} = \frac {10}{1},$则v_主(EG) : v_制(DEG) = 11 : 1,c正确;选择适当催化剂可以提高主反应的选择性,从而提高乙二醇的最终产率,d正确。
(2)①由题目信息知,该反应为气体分子数减小的反应,同一温度下,增大压强,平衡正向移动,则$\alpha$增大,故$L_1、$$L_2、$$L_3$分别代表$\alpha = 0.6、$0.5、0.4的曲线。②由图可知,压强相等时,温度越高则对应的平衡转化率$\alpha$越小,即平衡逆向移动,故该反应为放热反应,$\Delta H < 0。$③M、N两点对应平衡转化率相等,则平衡时各组分物质的量分数均相等,故K_x(M) = K_x(N);D点对应的平衡转化率为0.5,根据题给信息知,该反应按化学计量比进料,设起始加入2 mol CO、$3 mol H_2,$列三段式:
$2CO(g) + 3H_2(g) \rightleftharpoons HOCH_2CH_2OH(g)$
$\begin{matrix}$
起始量/mol & 2 & 3 & 0 \\
转化量/mol & 1 & 1.5 & 0.5 \\
平衡量/mol & 1 & 1.5 & 0.5 \\
$\end{matrix}$
平衡时$x(CO) = \frac {1}{3}、$$x(H_2) = \frac {1}{2}、$$x(HOCH_2CH_2OH) = \frac {1}{6},$则D点对应体系的$K_x = \frac {1}{6} × ( \frac {1}{3} )^2 × ( \frac {1}{2} )^3 = 12。$④设在该条件下,起始时加入$( \frac {1}{3} )^2 × ( \frac {1}{2} )^3 mmol CO$和$3 mol H_2,$$\alpha(H_2) = 0.75,$则$H_2$转化了2.25 mol,由此列三段式:
$2CO(g) + 3H_2(g) \rightleftharpoons HO CH_2CH_2OH(g)$
$\begin{matrix}$
起始量/mol & m & 3 & 0 \\
转化量/mol & 1.5 & 2.25 & 0.75 \\
平衡量/mol & m - 1.5 & 0.75 & 0.75 \\
$\end{matrix}$
平衡时$x(CO) = \frac {m - 1.5}{m}、$$x(H_2) = \frac {0.75}{m}、$$x(HOCH_2CH_2OH) = \frac {0.75}{m},$
则$K_p = \frac { \frac {0.75}{m} p_0 × ( \frac {0.75}{m} p_0 )^2}{( \frac {m - 1.5}{m} p_0 )^2 × ( \frac {0.75}{m} p_0 )^3} MPa^{-4} = \frac { \frac {1}{(m - 1.5)^2 p_0^2} × \frac {0.75^3}{m^3} p_0^3 }{ \frac {(0.75)^3}{m^3} p_0^3 } MPa^{-4}。$
(1)①0.05 ②cd
$(2)①L_1 $该反应为气体分子数减小的反应,温度相同时,增大压强,平衡正向移动,固定平衡转化率增大 ②< ③= 12
$ ④\frac {(m - 1.5)^2}{m p_o} × ( \frac {0.75}{m p_o} )^2$
解析:
(1)①环氧乙烷的初始浓度为$1.5 mol · L^{-1},$反应30 min,环氧乙烷完全转化,则0∼30 min内,v_总$(EO) = \frac {\Delta c_总(EO)}{\Delta t} = \frac {1.5 mol · L^{-1}}{30 min} = 0.05 mol · L^{-1} · min^{-1}。$②主反应$\Delta H $< 0,为放热反应,生成物总能量低于反应物总能量,a错误;由题目信息知,合成乙二醇的过程中伴随着副反应的发生,EG既是主反应的生成物,又是副反应的反应物,即EG的浓度变化量小于EO的浓度变化量,故v_总(EO) > v_总(EG),b错误;由题目信息知,反应完成后产物中n(EG) : n(DEG) = 10 : 1,即$\Delta n(EG) : \Delta n(DEG) = 10 : 1,$反应时间相同,则v_总(EG) : v_制(DEG) = 10 : 1,结合v_总(EG) = v_主(EG) - v_制(EG)可得,$\frac {v_主(EG) - v_制(EG)}{v_制(DEG)} = \frac {10}{1},$则v_主(EG) : v_制(DEG) = 11 : 1,c正确;选择适当催化剂可以提高主反应的选择性,从而提高乙二醇的最终产率,d正确。
(2)①由题目信息知,该反应为气体分子数减小的反应,同一温度下,增大压强,平衡正向移动,则$\alpha$增大,故$L_1、$$L_2、$$L_3$分别代表$\alpha = 0.6、$0.5、0.4的曲线。②由图可知,压强相等时,温度越高则对应的平衡转化率$\alpha$越小,即平衡逆向移动,故该反应为放热反应,$\Delta H < 0。$③M、N两点对应平衡转化率相等,则平衡时各组分物质的量分数均相等,故K_x(M) = K_x(N);D点对应的平衡转化率为0.5,根据题给信息知,该反应按化学计量比进料,设起始加入2 mol CO、$3 mol H_2,$列三段式:
$2CO(g) + 3H_2(g) \rightleftharpoons HOCH_2CH_2OH(g)$
$\begin{matrix}$
起始量/mol & 2 & 3 & 0 \\
转化量/mol & 1 & 1.5 & 0.5 \\
平衡量/mol & 1 & 1.5 & 0.5 \\
$\end{matrix}$
平衡时$x(CO) = \frac {1}{3}、$$x(H_2) = \frac {1}{2}、$$x(HOCH_2CH_2OH) = \frac {1}{6},$则D点对应体系的$K_x = \frac {1}{6} × ( \frac {1}{3} )^2 × ( \frac {1}{2} )^3 = 12。$④设在该条件下,起始时加入$( \frac {1}{3} )^2 × ( \frac {1}{2} )^3 mmol CO$和$3 mol H_2,$$\alpha(H_2) = 0.75,$则$H_2$转化了2.25 mol,由此列三段式:
$2CO(g) + 3H_2(g) \rightleftharpoons HO CH_2CH_2OH(g)$
$\begin{matrix}$
起始量/mol & m & 3 & 0 \\
转化量/mol & 1.5 & 2.25 & 0.75 \\
平衡量/mol & m - 1.5 & 0.75 & 0.75 \\
$\end{matrix}$
平衡时$x(CO) = \frac {m - 1.5}{m}、$$x(H_2) = \frac {0.75}{m}、$$x(HOCH_2CH_2OH) = \frac {0.75}{m},$
则$K_p = \frac { \frac {0.75}{m} p_0 × ( \frac {0.75}{m} p_0 )^2}{( \frac {m - 1.5}{m} p_0 )^2 × ( \frac {0.75}{m} p_0 )^3} MPa^{-4} = \frac { \frac {1}{(m - 1.5)^2 p_0^2} × \frac {0.75^3}{m^3} p_0^3 }{ \frac {(0.75)^3}{m^3} p_0^3 } MPa^{-4}。$
3. (2025·广东卷)钛单质及其化合物在航空、航天、催化等领域应用广泛。
(1)基态$Ti$原子的价层电子排布式为
(2)$298\ K$下,反应${TiO_{2}(s) + 2C(s) + 2Cl_{2}(g)\xlongequal{}TiCl_{4}(g) + 2CO(g)}$的$\Delta H<0$、$\Delta S>0$,则$298\ K$下该反应
(3)以$TiCl_{4}$为原料可制备$TiCl_{3}$。将$5.0\ mol\ TiCl_{4}$与$10.0\ mol\ Ti$放入容积为$V_{0}\ L$的恒容密闭容器中,反应体系存在下列过程。

①$\Delta H_{1}=$
②不同温度下,平衡时反应体系的组成如图。曲线Ⅰ对应的物质为

③温度$T_{0}\ K$下,$n[{TiCl_{4}(g)]}=$
(4)钛基催化剂可以催化储氢物质肼($N_{2}H_{4}$)的分解反应:
(e)${N_{2}H_{4}\xlongequal{}N_{2} + 2H_{2}}$
(f)${3N_{2}H_{4}\xlongequal{}N_{2} + 4NH_{3}}$
为研究某钛基催化剂对上述反应的影响,以肼的水溶液为原料(含$N_{2}H_{4}$的物质的量为$n_{0}$),进行实验,得到$n_{1}/n_{0}$、$n_{2}/n_{0}$随时间$t$变化的曲线如图。其中,$n_{1}$为${H_{2}}$与${N_{2}}$的物质的量之和;$n_{2}$为剩余$N_{2}H_{4}$的物质的量。
设$n_{e}$为$0\sim t$时间段内反应(e)消耗$N_{2}H_{4}$的物质的量,该时间段内,本体系中催化剂的选择性用$\frac{n_{e}}{n_{0}-n_{2}}×100\%$表示。
①$0\sim t_{0}\ min$内,$N_{2}H_{4}$的转化率为
②$0\sim t_{0}\ min$内,催化剂的选择性为

(1)基态$Ti$原子的价层电子排布式为
3d²4s²
。(2)$298\ K$下,反应${TiO_{2}(s) + 2C(s) + 2Cl_{2}(g)\xlongequal{}TiCl_{4}(g) + 2CO(g)}$的$\Delta H<0$、$\Delta S>0$,则$298\ K$下该反应
能
(填“能”或“不能”)自发进行。(3)以$TiCl_{4}$为原料可制备$TiCl_{3}$。将$5.0\ mol\ TiCl_{4}$与$10.0\ mol\ Ti$放入容积为$V_{0}\ L$的恒容密闭容器中,反应体系存在下列过程。

①$\Delta H_{1}=$
−267.8
$\ kJ·mol^{-1}$。②不同温度下,平衡时反应体系的组成如图。曲线Ⅰ对应的物质为
TiCl₂(s)
。
③温度$T_{0}\ K$下,$n[{TiCl_{4}(g)]}=$
0.5
$\ mol$,反应(c)的平衡常数$K=$$\frac{( \frac{6.0}{V_0} )^4}{( \frac{0.5}{V_0} )^3}$
$$(列出算式,无须化简)。(4)钛基催化剂可以催化储氢物质肼($N_{2}H_{4}$)的分解反应:
(e)${N_{2}H_{4}\xlongequal{}N_{2} + 2H_{2}}$
(f)${3N_{2}H_{4}\xlongequal{}N_{2} + 4NH_{3}}$
为研究某钛基催化剂对上述反应的影响,以肼的水溶液为原料(含$N_{2}H_{4}$的物质的量为$n_{0}$),进行实验,得到$n_{1}/n_{0}$、$n_{2}/n_{0}$随时间$t$变化的曲线如图。其中,$n_{1}$为${H_{2}}$与${N_{2}}$的物质的量之和;$n_{2}$为剩余$N_{2}H_{4}$的物质的量。
设$n_{e}$为$0\sim t$时间段内反应(e)消耗$N_{2}H_{4}$的物质的量,该时间段内,本体系中催化剂的选择性用$\frac{n_{e}}{n_{0}-n_{2}}×100\%$表示。
①$0\sim t_{0}\ min$内,$N_{2}H_{4}$的转化率为
1−y₂
(用含$y_{2}$的代数式表示)。②$0\sim t_{0}\ min$内,催化剂的选择性为
$\frac{3y₁+y₂−1}{8(1−y₂)}×100%$
(用含$y_{1}$与$y_{2}$的代数式表示,写出推导过程)。
答案:
$(1)3d^24s^2 (2)$能
(3)①−267.8
$②TiCl_2(s) ③0.5$
$(4)①1−y_2 ②$设$t_0 min$时,反应(e)转化的$N_2H_4$的物质的量为e,反应(f)转化的$N_2H_4$的物质的量为3f,存在如下转化关系:
$N_2H_4 \rightleftharpoons N_2 + 2H_2$
转化量:e e 2e
$3N_2H_4 \rightleftharpoons N_2 + 4NH_3$
转化量 3f f 4f
则$n_1 = 3e + f、$$n_2 = n_0 − (e + 3f)$
$\frac {3e + f}{n_0} = y_1 ·s ·s ①$
$\frac {n_0 - (e + 3f)}{n_0} = y_2 ·s ·s ②$
联立①②可得$e = \frac {3y_1 + y_2 - 1}{8} n_0,$$f = \frac {3 - y_1 - 3y_2}{8} n_0$
则$0 ∼ t_0 min$时,催化剂的选择性为$\frac {e}{e + 3f} × 100\% = \frac { \frac {3y_1 + y_2 - 1}{8(1 - y_2)} } × 100\%$
解析:
(1)Ti为第四周期ⅣB族元素,故基态Ti原子的价层电子排布式是$3d^24s^2。$$(2)\Delta H − T\Delta S $< 0时反应能自发进行,而由已知信息可知,该反应的\Delta H < 0、\Delta S > 0,该反应的$\Delta H − T\Delta S < 0$恒成立,故该反应在298 K时能自发进行。
(3)①根据反应(a)、(b)、(c)的物质转化关系,由盖斯定律可知,(c)−2(b) = (a),故$\Delta H_1 = +132.4 kJ · mol^{-1} − 2 × 200.1 kJ · mol^{-1} = −267.8 kJ · mol^{-1}。$②反应(a)为放热反应,反应(b)为吸热反应,故随着温度升高,$TiCl_2(s)$的物质的量减少,故曲线Ⅰ代表的物质是$TiCl_2(s)。$③平衡体系中的物质有$TiCl_4(g)、$$TiCl_3(g)、$Ti(s)、$TiCl_2(s)、$$TiCl_3(s),$结合上述分析及题图可知,曲线Ⅱ应代表$TiCl_3(g),$且$T_0 K$下$TiCl_2(s)、$$TiCl_3(s)$的物质的量均为0,根据投料情况知,Ti元素共15 mol,Cl元素共20 mol,则根据元素守恒及题中数据可得,$T_0 K$下$n[TiCl_4(g)] = 0.5 mol。$反应(c)的平衡常数$K = \frac {c^4(TiCl_3, g)}{c^3(TiCl_4, g)} = \frac {[ \frac {n(TiCl_3, g)}{V_0} ]^4}{[ \frac {n(TiCl_4, g)}{V_0} ]^3} = \frac {( \frac {6.0}{V_0} )^4}{( \frac {0.5}{V_0} )^3}。$
(4)①根据题意及图像可知,$0 ∼ t_0 min$内,$y_1 = \frac {n(H_2) + n(N_2)}{n(N_2H_4)},$$y_2 = \frac {n_剩余(N_2H_4)}{n(N_2H_4)},$故$0 ∼ t_0 min$内,$N_2H_4$的转化率为$1 − y_2。$②初始加入$N_2H_4$的物质的量为$n_0,$$0 ∼ t_0 min$内,设反应(e)消耗的$N_2H_4$的物质的量为e,反应(f)消耗的$N_2H_4$的物质的量为3f,则存在如下转化关系:
$N_2H_4 \rightleftharpoons N_2 + 2H_2$
转化量:e e 2e
$3N_2H_4 \rightleftharpoons N_2 + 4NH_3$
转化量 3f f 4f
故$\frac {3e + f}{n_0} = y_1,$$\frac {n_0 - e - 3f}{n_0} = y_2,$两式联立可得催化剂的选择性为$\frac {e}{e + 3f} × 100\% = \frac {3y_1 + y_2 - 1}{8(1 - y_2)} × 100\%。$
(3)①−267.8
$②TiCl_2(s) ③0.5$
$(4)①1−y_2 ②$设$t_0 min$时,反应(e)转化的$N_2H_4$的物质的量为e,反应(f)转化的$N_2H_4$的物质的量为3f,存在如下转化关系:
$N_2H_4 \rightleftharpoons N_2 + 2H_2$
转化量:e e 2e
$3N_2H_4 \rightleftharpoons N_2 + 4NH_3$
转化量 3f f 4f
则$n_1 = 3e + f、$$n_2 = n_0 − (e + 3f)$
$\frac {3e + f}{n_0} = y_1 ·s ·s ①$
$\frac {n_0 - (e + 3f)}{n_0} = y_2 ·s ·s ②$
联立①②可得$e = \frac {3y_1 + y_2 - 1}{8} n_0,$$f = \frac {3 - y_1 - 3y_2}{8} n_0$
则$0 ∼ t_0 min$时,催化剂的选择性为$\frac {e}{e + 3f} × 100\% = \frac { \frac {3y_1 + y_2 - 1}{8(1 - y_2)} } × 100\%$
解析:
(1)Ti为第四周期ⅣB族元素,故基态Ti原子的价层电子排布式是$3d^24s^2。$$(2)\Delta H − T\Delta S $< 0时反应能自发进行,而由已知信息可知,该反应的\Delta H < 0、\Delta S > 0,该反应的$\Delta H − T\Delta S < 0$恒成立,故该反应在298 K时能自发进行。
(3)①根据反应(a)、(b)、(c)的物质转化关系,由盖斯定律可知,(c)−2(b) = (a),故$\Delta H_1 = +132.4 kJ · mol^{-1} − 2 × 200.1 kJ · mol^{-1} = −267.8 kJ · mol^{-1}。$②反应(a)为放热反应,反应(b)为吸热反应,故随着温度升高,$TiCl_2(s)$的物质的量减少,故曲线Ⅰ代表的物质是$TiCl_2(s)。$③平衡体系中的物质有$TiCl_4(g)、$$TiCl_3(g)、$Ti(s)、$TiCl_2(s)、$$TiCl_3(s),$结合上述分析及题图可知,曲线Ⅱ应代表$TiCl_3(g),$且$T_0 K$下$TiCl_2(s)、$$TiCl_3(s)$的物质的量均为0,根据投料情况知,Ti元素共15 mol,Cl元素共20 mol,则根据元素守恒及题中数据可得,$T_0 K$下$n[TiCl_4(g)] = 0.5 mol。$反应(c)的平衡常数$K = \frac {c^4(TiCl_3, g)}{c^3(TiCl_4, g)} = \frac {[ \frac {n(TiCl_3, g)}{V_0} ]^4}{[ \frac {n(TiCl_4, g)}{V_0} ]^3} = \frac {( \frac {6.0}{V_0} )^4}{( \frac {0.5}{V_0} )^3}。$
(4)①根据题意及图像可知,$0 ∼ t_0 min$内,$y_1 = \frac {n(H_2) + n(N_2)}{n(N_2H_4)},$$y_2 = \frac {n_剩余(N_2H_4)}{n(N_2H_4)},$故$0 ∼ t_0 min$内,$N_2H_4$的转化率为$1 − y_2。$②初始加入$N_2H_4$的物质的量为$n_0,$$0 ∼ t_0 min$内,设反应(e)消耗的$N_2H_4$的物质的量为e,反应(f)消耗的$N_2H_4$的物质的量为3f,则存在如下转化关系:
$N_2H_4 \rightleftharpoons N_2 + 2H_2$
转化量:e e 2e
$3N_2H_4 \rightleftharpoons N_2 + 4NH_3$
转化量 3f f 4f
故$\frac {3e + f}{n_0} = y_1,$$\frac {n_0 - e - 3f}{n_0} = y_2,$两式联立可得催化剂的选择性为$\frac {e}{e + 3f} × 100\% = \frac {3y_1 + y_2 - 1}{8(1 - y_2)} × 100\%。$
查看更多完整答案,请扫码查看


