《2025年课时练人民教育出版社七年级数学上册人教版增强版》

【例2】一组按规律排列的数：$2$,$-4$,$8$,$-16$,$32$,…$$,则第$2024$个数是多少？
解：
【规律方法】
解决与乘方有关的规律问题的一般思路
(1)一般从符号和绝对值两个方面入手分析。
(2)由特殊到一般,归纳得出规律。

答案： 解:$-2^{2024}$.

3. 先阅读下列算式,再回答问题。
(1)$1^{2}+2× 1× 2+2^{2}= (1 + 2)^{2}$；
(2)$2^{2}+2× 2× 3+3^{2}= (2 + 3)^{2}$；
(3)$3^{2}+2× 3× 4+4^{2}= (3 + 4)^{2}$。
利用你发现的规律求$8^{2}+2× 8× 9+9^{2}$的结果是____。

答案： 289

1. $(-2)^{2}+2^{2}= $( )

A.$0$
B.$2$
C.$4$
D.$8$

答案： D

2. 下列各式的运算结果为正数的是( )

A.$-2^{4}× 5$
B.$(1 - 2)÷ 5$
C.$(1 - 2^{4})× (-5)$
D.$1 - (3× 5)^{6}$

答案： C

3. 计算：$-2^{4}÷ \frac{4}{9}× \left(-\frac{3}{2}\right)^{2}$等于( )

A.$-16$
B.$-81$
C.$16$
D.$81$

答案： B

4. 如图,按照操作步骤,若输入$x的值为5$,则输出的值为____。
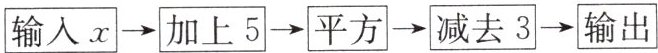
$\boxed{输入x}\to\boxed{加上5}\to\boxed{平方}\to\boxed{减去3}\to\boxed{输出}$

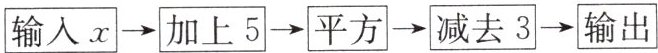
答案： 97

5. 已知$2+\frac{2}{3}= 2^{2}× \frac{2}{3}$,$3+\frac{3}{8}= 3^{2}× \frac{3}{8}$,$4+\frac{4}{15}= 4^{2}× \frac{4}{15}$,……$$,若$8+\frac{a}{b}= 8^{2}× \frac{a}{b}$($a$,$b$为正整数),则$a + b= $____。

答案： 71

6. 计算：
(1)$2× (-5)+2^{2}-3÷ \frac{1}{2}$；
(2)$(-2)^{2}+[18 - (-3)× 2]÷ 4$；
(3)$2× [5 + (-2)^{3}]-\left(-|-4|÷ \frac{1}{2}\right)$；
(4)$-2^{3}÷ \frac{8}{9}× \left(-\frac{1}{3}\right)^{2}-(-1)^{7}$；
(5)$(-1)^{4}-(1 - 0.5)× \frac{1}{3}× [2 - (-2)^{2}]$；
(6)$-1^{1018}-(1 - 0.5)× \frac{1}{3}× [2 - (-3)^{2}]$。

答案： 解:
(1)-12.
(2)10.
(3)2.
(4)0.
(5)$1\frac{1}{3}$.
(6)$\frac{1}{6}$.