《2025年同步练习西南大学出版社六年级数学上册西师大版河南专版》

(1)(圆上)任意一点到(圆心)的距离是半径。

答案： 圆上，圆心

(2)在同一个圆中,直径是半径的(2倍),直径用字母(d)来表示,半径用字母(r)来表示,圆的周长用字母(C)来表示,圆的面积用字母(S)来表示。

答案： $2$倍，$d$，$r$，$C$，$S$

(3)一个圆的半径是$4\mathrm{cm}$,它的周长是(25.12cm),面积是(50.24cm²)。

答案： 25.12cm，50.24cm²

2. 根据条件解答。
(1)在一个圆中,$d = 0.6\mathrm{m}$,求$C和S$。
(2)在一个圆中,$r = 20\mathrm{m}$,求$C和S$。
(3)在一个圆中,$C = 25.12\mathrm{m}$,求$S$。

答案：
(1)$C = 1.884m$，$S = 0.2826m^{2}$；
(2)$C = 125.6m$，$S = 1256m^{2}$；
(3)$S = 50.24m^{2}$。

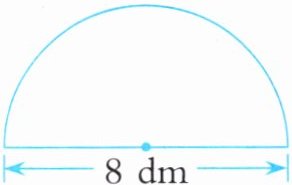
3. 求下面图形的周长和面积。

答案： 周长：
半圆直径：$ d = 8 \, dm $
半圆周长（含直径）：$ C = \frac{1}{2} × \pi d + d $
代入数据：$ C = \frac{1}{2} × 3.14 × 8 + 8 = 12.56 + 8 = 20.56 \, dm $
面积：
半圆半径：$ r = \frac{d}{2} = 4 \, dm $
半圆面积：$ S = \frac{1}{2} × \pi r^2 $
代入数据：$ S = \frac{1}{2} × 3.14 × 4^2 = \frac{1}{2} × 3.14 × 16 = 25.12 \, dm^2 $
结论：周长为 $ 20.56 \, dm $，面积为 $ 25.12 \, dm^2 $。

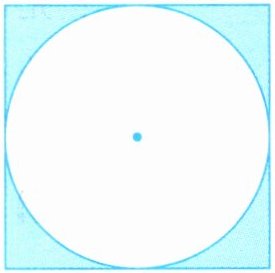
4. 下图中,正方形的周长为$16\mathrm{cm}$,圆的周长是多少？阴影部分的面积是多少？

答案： 正方形的周长为$16\mathrm{cm}$，则边长为：
$16 ÷ 4 = 4 \mathrm{cm}$。
圆的直径等于正方形的边长，即$4 \mathrm{cm}$，半径为：
$4 ÷ 2 = 2 \mathrm{cm}$。
圆的周长为：
$2 × \pi × 2 = 12.56 \mathrm{cm}$（$\pi$取$3.14$）。
正方形的面积为：
$4 × 4 = 16 \mathrm{cm^2}$。
圆的面积为：
$\pi × 2^2 = 12.56 \mathrm{cm^2}$（$\pi$取$3.14$）。
阴影部分的面积为正方形面积减去圆的面积：
$16 - 12.56 = 3.44 \mathrm{cm^2}$。
综上，圆的周长是$12.56 \mathrm{cm}$，阴影部分的面积是$3.44 \mathrm{cm^2}$。

5. 广场中心有一个直径为$10\mathrm{m}$的圆形喷泉池,喷泉池外围有一条宽为$1\mathrm{m}$的环形小路。小路的面积是多少平方米？

答案： 内圆半径：$10÷2 = 5(m)$
外圆半径：$5 + 1= 6(m)$
内圆面积：$3.14×5^{2}=3.14×25 = 78.5(m^{2})$
外圆面积：$3.14×6^{2}=3.14×36 = 113.04(m^{2})$
小路面积：$113.04 - 78.5 = 34.54(m^{2})$
答：小路的面积是$34.54$平方米。

6. 有一个圆柱形木桶,底面直径为$50\mathrm{cm}$。现在为这个木桶加两道铁箍,每道铁箍的接头处要用掉铁丝$25\mathrm{cm}$。一共需要铁丝多少厘米？

答案： 1. 计算底面圆的周长：$C = \pi d = 3.14 × 50 = 157$（cm）
2. 每道铁箍所需铁丝长度：$157 + 25 = 182$（cm）
3. 两道铁箍共需铁丝：$182 × 2 = 364$（cm）
答：一共需要铁丝364厘米。