2025年同步练习西南大学出版社六年级数学上册西师大版河南专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年同步练习西南大学出版社六年级数学上册西师大版河南专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
(1)车轮滚动一圈,所行的路程是车轮的(
A.半径
B.直径
C.周长
D.面积
C
)。A.半径
B.直径
C.周长
D.面积
答案:
C
(2)求圆形花坛所占地面的大小,是求圆的(
A.半径
B.直径
C.周长
D.面积
D
)。A.半径
B.直径
C.周长
D.面积
答案:
D
(3)圆的周长为6.28cm,这个圆的面积是(
$A.6.28cm^2$
B.6.28cm
C.3.14cm
D.$3.14cm^2$
D
)。$A.6.28cm^2$
B.6.28cm
C.3.14cm
D.$3.14cm^2$
答案:
D
2. 填表。(单位:cm)
|半径|直径|周长|面积|
|----|----|----|----|
|
|
|
|半径|直径|周长|面积|
|----|----|----|----|
|
5
|10
|31.4
|78.5
||
3
|6
|18.84
|28.26
||
0.5
|1
|3.14
|0.785
|
答案:
1. 半径=5cm
直径:5×2=10cm
周长:3.14×10=31.4cm
面积:3.14×5²=78.5cm²
2. 直径=6cm
半径:6÷2=3cm
周长:3.14×6=18.84cm
面积:3.14×3²=28.26cm²
3. 周长=3.14cm
直径:3.14÷3.14=1cm
半径:1÷2=0.5cm
面积:3.14×0.5²=0.785cm²
|半径|直径|周长|面积|
|----|----|----|----|
|5|10|31.4|78.5|
|3|6|18.84|28.26|
|0.5|1|3.14|0.785|
直径:5×2=10cm
周长:3.14×10=31.4cm
面积:3.14×5²=78.5cm²
2. 直径=6cm
半径:6÷2=3cm
周长:3.14×6=18.84cm
面积:3.14×3²=28.26cm²
3. 周长=3.14cm
直径:3.14÷3.14=1cm
半径:1÷2=0.5cm
面积:3.14×0.5²=0.785cm²
|半径|直径|周长|面积|
|----|----|----|----|
|5|10|31.4|78.5|
|3|6|18.84|28.26|
|0.5|1|3.14|0.785|
3. 在下面的方格纸上各画一个最大的圆,再算出圆的面积。(每个小方格的边长为0.4cm。)
(1)
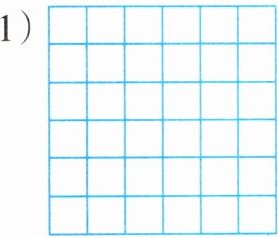
(2)

(1)

(2)

答案:
1. (1)
解:观察方格纸,可知这个正方形方格纸中最大圆的直径等于正方形的边长,这里边长为$0.4×6 = 2.4\mathrm{cm}$,则半径$r=\frac{2.4}{2}=1.2\mathrm{cm}$。
根据圆的面积公式$S = \pi r^{2}$($\pi$取$3.14$),可得$S = 3.14×1.2^{2}=3.14×1.44 = 4.5216\mathrm{cm}^{2}$。
2. (2)
解:观察方格纸,可知这个长方形方格纸中最大圆的直径等于长方形的宽,宽为$0.4×5 = 2\mathrm{cm}$,则半径$r = \frac{2}{2}=1\mathrm{cm}$。
根据圆的面积公式$S=\pi r^{2}$($\pi$取$3.14$),可得$S = 3.14×1^{2}=3.14\mathrm{cm}^{2}$。
综上,(1)中圆的面积是$4.5216\mathrm{cm}^{2}$;(2)中圆的面积是$3.14\mathrm{cm}^{2}$。
解:观察方格纸,可知这个正方形方格纸中最大圆的直径等于正方形的边长,这里边长为$0.4×6 = 2.4\mathrm{cm}$,则半径$r=\frac{2.4}{2}=1.2\mathrm{cm}$。
根据圆的面积公式$S = \pi r^{2}$($\pi$取$3.14$),可得$S = 3.14×1.2^{2}=3.14×1.44 = 4.5216\mathrm{cm}^{2}$。
2. (2)
解:观察方格纸,可知这个长方形方格纸中最大圆的直径等于长方形的宽,宽为$0.4×5 = 2\mathrm{cm}$,则半径$r = \frac{2}{2}=1\mathrm{cm}$。
根据圆的面积公式$S=\pi r^{2}$($\pi$取$3.14$),可得$S = 3.14×1^{2}=3.14\mathrm{cm}^{2}$。
综上,(1)中圆的面积是$4.5216\mathrm{cm}^{2}$;(2)中圆的面积是$3.14\mathrm{cm}^{2}$。
4. 周长是37.2m的圆形喷水池,占地面积是多少平方米?($\pi$取3.1。)
答案:
已知圆形喷水池周长为$37.2m$,$\pi$取$3.1$。
根据圆的周长公式$C = 2\pi r$,可得半径$r = C÷(2\pi)$,将$C = 37.2$,$\pi = 3.1$代入可得:
$r = 37.2÷(2×3.1)$
$= 37.2÷6.2$
$= 6(m)$
根据圆的面积公式$S = \pi r^{2}$,将$r = 6$,$\pi = 3.1$代入可得:
$S = 3.1×6^{2}$
$= 3.1×36$
$= 111.6(m^{2})$
答:占地面积是$111.6$平方米。
根据圆的周长公式$C = 2\pi r$,可得半径$r = C÷(2\pi)$,将$C = 37.2$,$\pi = 3.1$代入可得:
$r = 37.2÷(2×3.1)$
$= 37.2÷6.2$
$= 6(m)$
根据圆的面积公式$S = \pi r^{2}$,将$r = 6$,$\pi = 3.1$代入可得:
$S = 3.1×6^{2}$
$= 3.1×36$
$= 111.6(m^{2})$
答:占地面积是$111.6$平方米。
5. 一个圆形花坛,直径是10m,这个花坛占地面积是多少平方米? 如果给这个花坛围上竹篱笆,竹篱笆长多少米?
答案:
答题卡:
已知圆形花坛直径$d = 10m$,则半径$r=\frac{d}{2}=\frac{10}{2}=5m$。
根据圆的面积公式$S=\pi r^{2}$,$\pi$取$3.14$,可得花坛占地面积$S = 3.14×5^{2}=3.14×25 = 78.5$(平方米)。
根据圆的周长公式$C = \pi d$,$\pi$取$3.14$,可得竹篱笆长(即圆周长)$C = 3.14×10 = 31.4$(米)。
答:这个花坛占地面积是$78.5$平方米,竹篱笆长$31.4$米。
已知圆形花坛直径$d = 10m$,则半径$r=\frac{d}{2}=\frac{10}{2}=5m$。
根据圆的面积公式$S=\pi r^{2}$,$\pi$取$3.14$,可得花坛占地面积$S = 3.14×5^{2}=3.14×25 = 78.5$(平方米)。
根据圆的周长公式$C = \pi d$,$\pi$取$3.14$,可得竹篱笆长(即圆周长)$C = 3.14×10 = 31.4$(米)。
答:这个花坛占地面积是$78.5$平方米,竹篱笆长$31.4$米。
6. (1)猜想:周长相等的长方形、正方形、圆中,谁的面积最大? 谁的面积最小?
(2)验证:周长为12.56cm的长方形、正方形、圆,它们的面积各是多少平方厘米?
(3)你得出了什么结论?
(2)验证:周长为12.56cm的长方形、正方形、圆,它们的面积各是多少平方厘米?
(3)你得出了什么结论?
答案:
(1) 猜想:圆的面积最大,长方形的面积最小。
(2) 验证:
设周长为 $C = 12.56cm$。
圆:
由圆的周长公式 $C = 2\pi r$,得半径 $r = \frac{C}{2\pi} = \frac{12.56}{2 × 3.14} = 2cm$。
圆的面积 $S_{圆} = \pi r^2 = 3.14 × 2^2 = 12.56cm^2$。
正方形:
由正方形的周长公式 $C = 4a$,得边长 $a = \frac{C}{4} = \frac{12.56}{4} = 3.14cm$。
正方形的面积 $S_{正方形} = a^2 = 3.14^2 = 9.8596cm^2$。
长方形:
设长方形的长为 $a$,宽为 $b$,且 $2(a + b) = 12.56$,即 $a + b = 6.28$。
由基本不等式 $a^2 + b^2 \geq 2ab$,得 $ab \leq \left(\frac{a + b}{2}\right)^2 = 3.14^2 = 9.8596$,当且仅当 $a = b$ 时取等号,但长方形长宽不等,所以面积小于正方形面积,一定小于$9.8596cm^2$,例如当长为$3.28$,宽为$3$时,面积为 $S_{长方形} =3.28×3= 9.84cm^2$。
(3) 结论:
周长相等的长方形、正方形、圆中,圆的面积最大,长方形的面积最小。
(1) 猜想:圆的面积最大,长方形的面积最小。
(2) 验证:
设周长为 $C = 12.56cm$。
圆:
由圆的周长公式 $C = 2\pi r$,得半径 $r = \frac{C}{2\pi} = \frac{12.56}{2 × 3.14} = 2cm$。
圆的面积 $S_{圆} = \pi r^2 = 3.14 × 2^2 = 12.56cm^2$。
正方形:
由正方形的周长公式 $C = 4a$,得边长 $a = \frac{C}{4} = \frac{12.56}{4} = 3.14cm$。
正方形的面积 $S_{正方形} = a^2 = 3.14^2 = 9.8596cm^2$。
长方形:
设长方形的长为 $a$,宽为 $b$,且 $2(a + b) = 12.56$,即 $a + b = 6.28$。
由基本不等式 $a^2 + b^2 \geq 2ab$,得 $ab \leq \left(\frac{a + b}{2}\right)^2 = 3.14^2 = 9.8596$,当且仅当 $a = b$ 时取等号,但长方形长宽不等,所以面积小于正方形面积,一定小于$9.8596cm^2$,例如当长为$3.28$,宽为$3$时,面积为 $S_{长方形} =3.28×3= 9.84cm^2$。
(3) 结论:
周长相等的长方形、正方形、圆中,圆的面积最大,长方形的面积最小。
查看更多完整答案,请扫码查看


