《2025年四清导航七年级数学上册湘教版》

9. (邵阳期中)下列写法正确的是(D)
A.$x5$
B.$4m× n$
C.$x(x + 1)\frac{3}{4}$
D.$-\frac{1}{2}ab$

答案： D

10. (开福期末)10月中旬,为了校体育文化节的顺利进行,学校体育组决定将跳远沙坑加长.若原来的沙坑长为$a$,宽为$b$,如果长增加$x$,那么新的沙坑增加的面积为(D)
A.$a(b + x)$
B.$b(a + x)$
C.$ax$
D.$bx$

答案： D

11. (道县期末)点$O$,$A$,$B$,$C$在数轴上的位置如图所示,其中点$A$,$B到原点O$的距离相等,点$A$,$C之间的距离为3$.若点$C表示的数为x$,则点$B$所表示的数为(C)

A.$x + 3$
B.$x - 3$
C.$-x + 3$
D.$-x - 3$
]

答案： C

12. (衡南县期末)一个两位数,个位数字为$a$,十位数字为$b$,则这个两位数为$10b+a$；
(变式)(新田县期中)一个三位数,中间的数字是$2$,百位数字和个位数字分别是$x和y$,这个三位数是$100x+20+y$.

答案： $10b+a$ (变式)$100x+20+y$

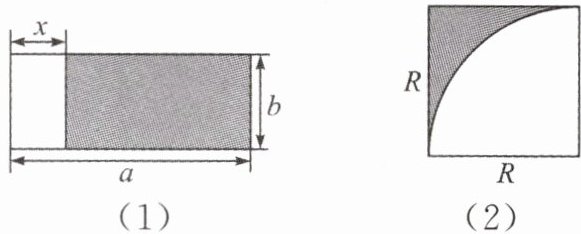
13. (教材 P66 练习 T4 变式)用字母表示图中阴影部分的面积.
]

答案：
(1)阴影部分的面积$=ab-bx$
(2)阴影部分的面积=$R^{2}-\frac {1}{4}πR^{2}$

14. (雨花区期中)小华坐公交车要投两元钱,他发现刷学生卡可以省钱,于是在公交总站办理了学生卡,充值了$50$元,如果小华乘车的次数用$n$表示,则记录他每次乘车后的余额$m$(元)如下表：

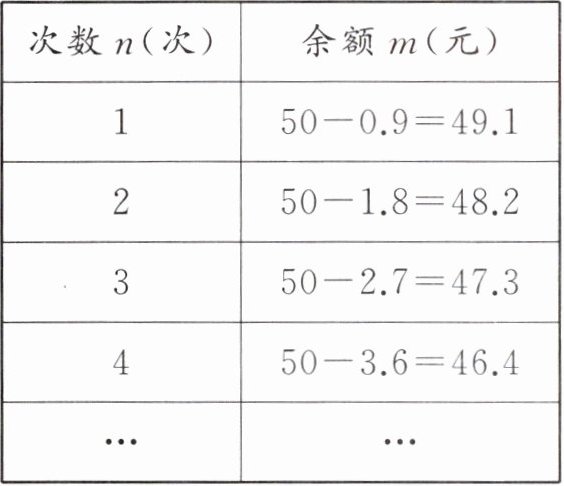
(1)小华乘车$8$次后的余额是多少元?
(2)写出用乘车的次数$n表示余额m$的式子.

答案：
(1)小华乘车8次后的余额是42.8元
(2)用乘车的次数n表示余额m的式子为$m=50-0.9n$

15. (对接新课标:图形的变化规律)(雨花区期中)某餐厅中$1张餐桌可坐6$人,有以下两种摆放方式：

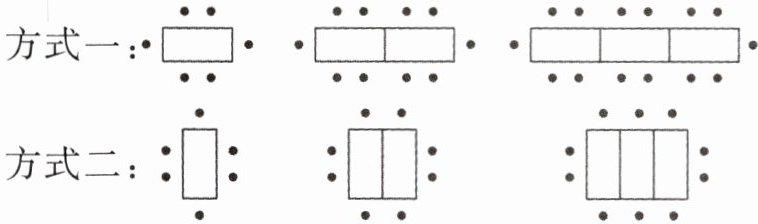
对于方式一,$4$张桌子拼在一起可坐多少人?$n$张桌子呢? 对于方式二呢?

答案： 方式一中,4张桌子可以坐18人,n张桌子可坐$(4n+2)$人;方式二中,4张桌子可坐12人,n张桌子可坐$(2n+4)$人