第48页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
13.计算:
(1)$(-2.8)+(-3.6)+(-1.5)+3.6$;
(2)$(-8)×(+3.67)×(-0.125)$;
(3)$-3^{2}÷(-2)^{2}×|-1\frac {1}{3}|×6+(-2)^{3}$.
(1)$(-2.8)+(-3.6)+(-1.5)+3.6$;
(2)$(-8)×(+3.67)×(-0.125)$;
(3)$-3^{2}÷(-2)^{2}×|-1\frac {1}{3}|×6+(-2)^{3}$.
答案:
(1)原式$=[(-2.8)+(-1.5)]+[(-3.6)+3.6]=-4.3+0=-4.3$;
(2)原式$=[(-8)×(-0.125)]×3.67=3.67$;
(3)原式$=-9÷4×\frac{4}{3}×6+(-8)=-18-8=-26$
(1)原式$=[(-2.8)+(-1.5)]+[(-3.6)+3.6]=-4.3+0=-4.3$;
(2)原式$=[(-8)×(-0.125)]×3.67=3.67$;
(3)原式$=-9÷4×\frac{4}{3}×6+(-8)=-18-8=-26$
14.计算:
(1)(张家界中考)$(-\frac {1}{2})-(-\frac {1}{3})+(-\frac {1}{4})$;
(2)(常德中考)$17-2^{3}÷(-2)×3$.
(1)(张家界中考)$(-\frac {1}{2})-(-\frac {1}{3})+(-\frac {1}{4})$;
(2)(常德中考)$17-2^{3}÷(-2)×3$.
答案:
(1)原式$=-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}=-\frac{5}{12}$;
(2)原式$=17-8÷(-2)×3=17+4×3=29$
(1)原式$=-\frac{1}{2}+\frac{1}{3}-\frac{1}{4}=-\frac{5}{12}$;
(2)原式$=17-8÷(-2)×3=17+4×3=29$
15.根据绝对值的几何意义可知:$|3|= |3-0|表示数轴上数3$对应的点到原点的距离,$|x-4|表示数轴上数x对应的点到数4$对应的点的距离,那么:
(1)$|x-1|$表示的几何意义是:
(2)你能求出$|x-1|+|x+2|$的最小值吗?请试一试.
(1)$|x-1|$表示的几何意义是:
数轴上数$x$对应的点到数1对应的点的距离
;(2)你能求出$|x-1|+|x+2|$的最小值吗?请试一试.
$|x-1|$表示数轴上数$x$对应的点到数1对应的点的距离,$|x+2|$表示数轴上数$x$对应的点到数-2对应的点的距离,所以$|x-1|+|x+2|$表示数轴上数$x$对应的点到数1和数-2对应的点的距离和.要使$|x-1|+|x+2|$的值最小,$x$的值只要取-2到1之间(包括-2,1)的任意一个数,当$x=1$时,$|x-1|+|x+2|=3$.所以$|x-1|+|x+2|$的最小值是3
答案:
(1)数轴上数$x$对应的点到数1对应的点的距离;
(2)$|x-1|$表示数轴上数$x$对应的点到数1对应的点的距离,$|x+2|$表示数轴上数$x$对应的点到数-2对应的点的距离,所以$|x-1|+|x+2|$表示数轴上数$x$对应的点到数1和数-2对应的点的距离和.要使$|x-1|+|x+2|$的值最小,$x$的值只要取-2到1之间(包括-2,1)的任意一个数,当$x=1$时,$|x-1|+|x+2|=3$.所以$|x-1|+|x+2|$的最小值是3
(1)数轴上数$x$对应的点到数1对应的点的距离;
(2)$|x-1|$表示数轴上数$x$对应的点到数1对应的点的距离,$|x+2|$表示数轴上数$x$对应的点到数-2对应的点的距离,所以$|x-1|+|x+2|$表示数轴上数$x$对应的点到数1和数-2对应的点的距离和.要使$|x-1|+|x+2|$的值最小,$x$的值只要取-2到1之间(包括-2,1)的任意一个数,当$x=1$时,$|x-1|+|x+2|=3$.所以$|x-1|+|x+2|$的最小值是3
16.(永州期中)小李同学在学习完有理数的运算后,对运算产生了浓厚的兴趣,他借助有理数的运算,定义一种新运算“☆”,运算规定:对于任意有理数$a,b$,都有$a☆b= |a+b|+|a-b|$,如$3☆4= |3+4|+|3-4|= 8$.
(1)计算$7☆(-2)$的值;
(2)计算$(-5)☆[1☆(-2)]$的值;
(3)当$a,b$在数轴上的位置如图所示时,化简$a☆b$.
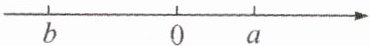
(1)计算$7☆(-2)$的值;
(2)计算$(-5)☆[1☆(-2)]$的值;
(3)当$a,b$在数轴上的位置如图所示时,化简$a☆b$.
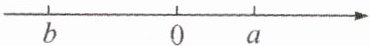
答案:
(1)由题意可得7☆$(-2)=|7+(-2)|+|7-(-2)|=5+9=14$;
(2)由题意可得$(-5)☆[1☆(-2)]=(-5)☆[|1+(-2)|+|1-(-2)|]=(-5)☆4=|(-5)+4|+|(-5)-4|=10$;
(3)根据数轴可得$a>0,b<0$且$a-b>0,a+b<0$,由题意可得$a☆b=|a+b|+|a-b|=-(a+b)+a-b=-2b$
(1)由题意可得7☆$(-2)=|7+(-2)|+|7-(-2)|=5+9=14$;
(2)由题意可得$(-5)☆[1☆(-2)]=(-5)☆[|1+(-2)|+|1-(-2)|]=(-5)☆4=|(-5)+4|+|(-5)-4|=10$;
(3)根据数轴可得$a>0,b<0$且$a-b>0,a+b<0$,由题意可得$a☆b=|a+b|+|a-b|=-(a+b)+a-b=-2b$
查看更多完整答案,请扫码查看


