《2025年同步练习册河北教育出版社五年级数学上册冀教版》

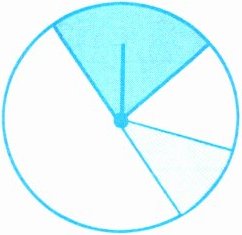
1. 转动下面的圆盘,指针指向哪个区域的可能性最大？指向哪个区域的可能性最小？在图上标出来。

答案： 解析：本题考查可能性的大小与区域面积大小之间的关系。在圆盘中，哪个区域的面积越大，指针指向该区域的可能性就越大；哪个区域的面积越小，指针指向该区域的可能性就越小。
答案：观察圆盘可知，图中最大的区域是左边的扇形区域，最小的区域是右下方的扇形区域。所以指针指向左边区域的可能性最大，指向右下方区域的可能性最小。图略（在左边区域标注“可能性最大”，在右下方区域标注“可能性最小” ）。

2. 按要求在圆盘上涂色。

答案： 解析：本题考查了可能性大小的判断。
第一个圆盘：指针一定停在红色区域，那么整个圆盘必须全部涂成红色。
第二个圆盘：指针停在黄色区域的可能性比停在红色区域的可能性大，那么黄色区域的面积要大于红色区域的面积。
可以将圆盘分成8等份，其中黄色区域涂5份，红色区域涂3份。
答案：第一个圆盘：全部涂成红色。
第二个圆盘：将圆盘分成8等份，其中黄色区域涂5份，红色区域涂3份。(答案不唯一，只要黄色区域面积大于红色区域面积即可)

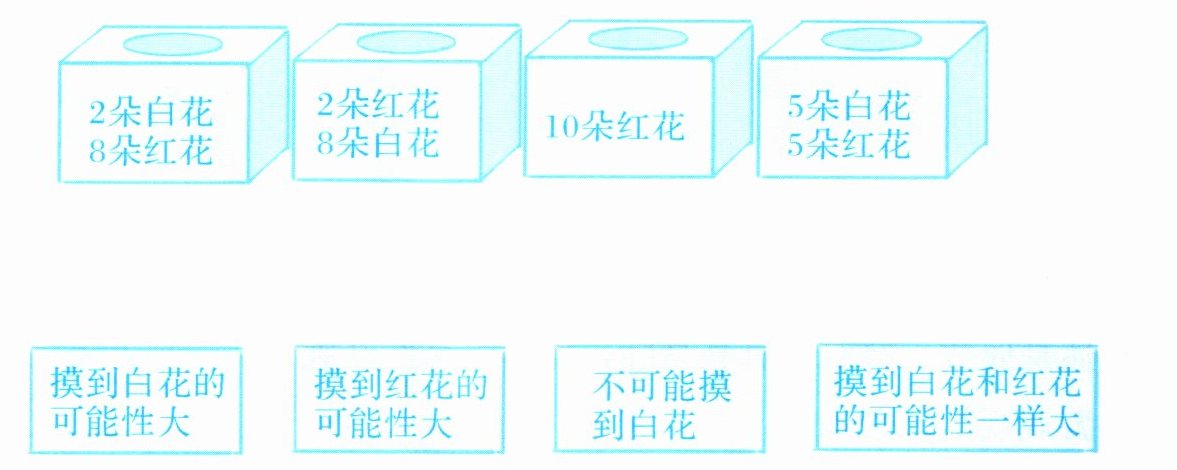
3. 连一连。
2朵白花
8朵红花　　　　2朵红花
8朵白花　　　　10朵红花　　　　5朵白花
5朵红花
摸到白花的可能性大　　　　摸到红花的可能性大　　　　不可能摸到白花　　　　摸到白花和红花的可能性一样大

答案： 解析：本题考查概率的基本概念，通过计算不同盒子中白花和红花的数量比例来判断摸到白花或红花的可能性大小。
答案：
第一个盒子：2朵白花，8朵红花，摸到红花的可能性大；
第二个盒子：2朵红花，8朵白花，摸到白花的可能性大；
第三个盒子：10朵红花，不可能摸到白花；
第四个盒子：5朵白花，5朵红花，摸到白花和红花的可能性一样大。

4. 聪聪和丫丫玩掷骰子游戏。

(1)这个游戏规则公平吗？
(2)请你制订一个公平的游戏规则。

答案：
(1) 解析：
考查知识点：游戏规则的公平性。
分析：骰子有$6$个面，分别标有$1$到$6$的点数。聪聪猜正面朝上是几点，猜对的概率是$\frac{1}{6}$，而丫丫获胜的概率是$1 - \frac{1}{6}=\frac{5}{6}$。
由于$\frac{1}{6} \neq \frac{5}{6}$，所以这个游戏规则不公平。
答案：这个游戏规则不公平。
(2) 解析：
考查知识点：设计公平的游戏规则。
分析：要制定一个公平的游戏规则，需要让双方获胜的概率相等。可以规定：如果正面朝上的点数是$1$、$2$、$3$，聪聪获胜；如果正面朝上的点数是$4$、$5$、$6$，丫丫获胜。这样双方获胜的概率都是$\frac{3}{6}=\frac{1}{2}$。
答案：公平的游戏规则可以是：如果正面朝上的点数是$1$、$2$、$3$，聪聪获胜；如果正面朝上的点数是$4$、$5$、$6$，丫丫获胜。（答案不唯一）。