《2025年同步练习册河北教育出版社五年级数学上册冀教版》

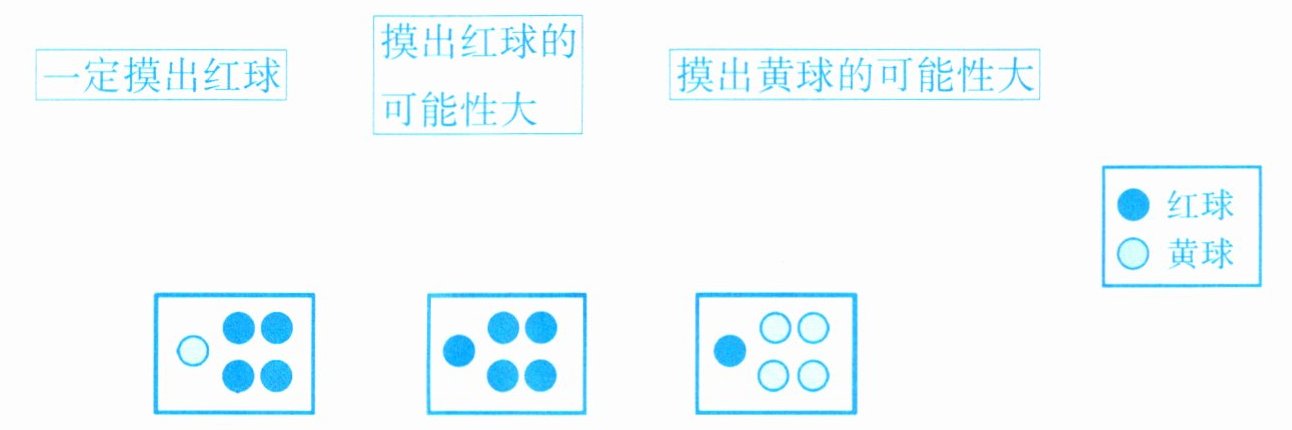
1. 根据摸球的可能性,判断是从哪个盒子里摸的,用线连起来。
一定摸出红球 摸出红球的可能性大 摸出黄球的可能性大
● 红球 ○ 黄球
□ ○●●● □ ●●●● □ ●○○○

答案： 本题可根据盒子中球的颜色及数量来判断摸出球的可能性情况。
第一个盒子中只有1个黄球和4个红球，红球的数量多于黄球，所以从这个盒子中摸出红球的可能性大。
第二个盒子中只有红球，所以从这个盒子中一定摸出红球。
第三个盒子中有1个红球和3个黄球，黄球的数量多于红球，所以从这个盒子中摸出黄球的可能性大。
连线如下：
一定摸出红球——□ ●●●●
摸出红球的可能性大——□ ○●●●
摸出黄球的可能性大——□ ●○○○

2. 小红准备在盒子中放若干黑、白棋子,再从盒子中摸出一枚棋子。
(1)要使摸出白棋子的可能性大,应该怎样放棋子？
(2)要使摸出的棋子一定是黑棋子,应该怎样放棋子？
(3)要使摸出黑、白棋子的可能性一样大,应该怎样放棋子？

答案： 解析：本题考查的是概率问题，根据概率公式，某种颜色棋子的数量越多，摸出的可能性就越大，反之则越小，如果两种颜色的棋子数量相等，则摸出的概率相等。
答案：
(1)要使摸出白棋子的可能性大，应该放的白棋子数量比黑棋子多。
(2)要使摸出的棋子一定是黑棋子，应该全部放黑棋子，不放白棋子。
(3)要使摸出黑、白棋子的可能性一样大，应该放的黑棋子和白棋子数量相等。

3. 亮亮和聪聪进行投球比赛,前6场的结果如下：

下场比赛谁获胜的可能性大？说出你判断的理由。

答案： 解析：本题考查概率相关知识，判断谁获胜的可能性大，需要根据两人之前的胜负情况来分析各自获胜的概率。
在前6场比赛中，亮亮胜了5场，负了1场；聪聪胜了1场，负了5场。
计算两人获胜的概率：
亮亮获胜的概率：$5÷6=\frac{5}{6}$
聪聪获胜的概率：$1÷6=\frac{1}{6}$
因为$\frac{5}{6} \gt \frac{1}{6}$，即亮亮获胜的概率大于聪聪获胜的概率。
答案：下场比赛亮亮获胜的可能性大。因为前6场比赛中亮亮获胜的场次远多于聪聪，亮亮获胜的概率为$\frac{5}{6}$，聪聪获胜的概率为$\frac{1}{6}$，亮亮获胜的概率大。

4. 有三个盒子,一个装有2个红球,一个装有2个白球,还有一个装有红球和白球各1个。现在三个盒子上的标签全贴错了。你能只从一个盒子里拿出1个球来,就确定这三个盒子里各装的是什么颜色的球吗？

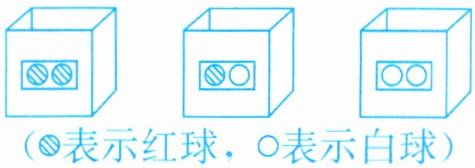
(●表示红球,○表示白球)

答案： 解析：本题考查的是逻辑推理能力。
可以从贴有“1红1白”标签的盒子中取出一个球，进行分析：
由于所有标签都贴错了，
如果从贴有“1红1白”标签的盒子中取出的是红球，那么这个盒子实际上装的是两个红球。
这样一来，原本贴有“2白”标签的盒子就不可能装两个白球了（因为所有标签都贴错了），它只能装“1红1白”。
而原本贴有“2红”标签的盒子，由于不能装两个红球（已被“1红1白”标签的盒子占据），也不能装“1红1白”（因为所有标签都贴错了），所以它只能装两个白球。
同理，如果从贴有“1红1白”标签的盒子中取出的是白球，那么这个盒子实际上装的是两个白球。
这样一来，原本贴有“2红”标签的盒子就不可能装两个红球了，它只能装“1红1白”。
而原本贴有“2白”标签的盒子，由于不能装两个白球（已被“1红1白”标签的盒子占据），也不能装“1红1白”（因为所有标签都贴错了），所以它只能装两个红球。
因此，只需从贴有“1红1白”标签的盒子中取出一个球，就可以确定这三个盒子里各装的是什么颜色的球了。
答案：从贴有“1红1白”标签的盒子中取出一个球：
如果取出的是红球，那么这个盒子实际上是“2红”，贴有“2白”标签的盒子实际上是“1红1白”，贴有“2红”标签的盒子实际上是“2白”。
如果取出的是白球，那么这个盒子实际上是“2白”，贴有“2红”标签的盒子实际上是“1红1白”，贴有“2白”标签的盒子实际上是“2红”。