(1)$48÷36= (48÷12):(36÷12)= (4):(3)$
$\frac{1}{3}÷\frac{5}{8}= (\frac{1}{3}×24):(\frac{5}{8}×24)= (8):(15)$
$\frac{1}{3}÷\frac{5}{8}= (\frac{1}{3}×24):(\frac{5}{8}×24)= (8):(15)$
答案:
(1)$48÷36= (48÷12):(36÷12)= 4:3$
$\frac{1}{3}÷\frac{5}{8}= (\frac{1}{3}×24):(\frac{5}{8}×24)= 8:15$
(1)$48÷36= (48÷12):(36÷12)= 4:3$
$\frac{1}{3}÷\frac{5}{8}= (\frac{1}{3}×24):(\frac{5}{8}×24)= 8:15$
(2)$12:18= 24:
36
= 4
÷6= \frac{2
}{3}= 0.2:0.3
$
答案:
解析:本题考查比的基本性质,比的前项和后项同时乘或除以相同的数($0$除外),比值不变。以及比与除法、分数之间的关系。
对于$12:18 = 24:( )$,因为$24÷12 = 2$,即前项乘以$2$,根据比的基本性质,后项也应乘以$2$,$18×2 = 36$,所以括号里应填$36$。
对于$12:18 = ( )÷6$,因为$6÷18=\frac{1}{3}$,即后项除以$3$,根据比的基本性质,前项也应除以$3$,$12÷3 = 4$,所以括号里应填$4$。
对于$12:18=\frac{( )}{3}$,因为$18÷3 = 6$,即后项除以$6$,根据比的基本性质,前项也应除以$6$,$12÷6 = 2$,所以括号里应填$2$。
对于$12:18 = 0.2:( )$,因为$0.2÷12=\frac{1}{60}$,即前项除以$60$,根据比的基本性质,后项也应除以$60$,$18÷60 = 0.3$,所以括号里应填$0.3$。
答案:$36$;$4$;$2$;$0.3$。
对于$12:18 = 24:( )$,因为$24÷12 = 2$,即前项乘以$2$,根据比的基本性质,后项也应乘以$2$,$18×2 = 36$,所以括号里应填$36$。
对于$12:18 = ( )÷6$,因为$6÷18=\frac{1}{3}$,即后项除以$3$,根据比的基本性质,前项也应除以$3$,$12÷3 = 4$,所以括号里应填$4$。
对于$12:18=\frac{( )}{3}$,因为$18÷3 = 6$,即后项除以$6$,根据比的基本性质,前项也应除以$6$,$12÷6 = 2$,所以括号里应填$2$。
对于$12:18 = 0.2:( )$,因为$0.2÷12=\frac{1}{60}$,即前项除以$60$,根据比的基本性质,后项也应除以$60$,$18÷60 = 0.3$,所以括号里应填$0.3$。
答案:$36$;$4$;$2$;$0.3$。
(3)小明下载资料,10 秒下载了 3.2 MB。下载量与下载时间的比是
3.2
:10
,化成最简整数比是8
:25
,比值是0.32
。
答案:
解析:题目考查比的意义,以及化简比和求比值的方法。
首先,根据题目给出的信息,下载量与下载时间的比是 3.2 MB : 10 s。
为了得到最简整数比,需要将 3.2 和 10 同时乘以一个适当的数,使得它们变成整数。
这里,可以将它们同时乘以 10(或者理解为将小数点向右移动一位),得到 32 : 100。
然后,对这个比进行化简。32 和 100 的最大公约数是 4,
所以,将 32 和 100 同时除以 4,得到最简整数比 8 : 25。
比值是前项除以后项的结果,即 3.2÷10=0.32,或者理解为 8÷25=0.32。
答案:
下载量与下载时间的比是 3.2 : 10,
化成最简整数比是 8 : 25,
比值是 0.32。
首先,根据题目给出的信息,下载量与下载时间的比是 3.2 MB : 10 s。
为了得到最简整数比,需要将 3.2 和 10 同时乘以一个适当的数,使得它们变成整数。
这里,可以将它们同时乘以 10(或者理解为将小数点向右移动一位),得到 32 : 100。
然后,对这个比进行化简。32 和 100 的最大公约数是 4,
所以,将 32 和 100 同时除以 4,得到最简整数比 8 : 25。
比值是前项除以后项的结果,即 3.2÷10=0.32,或者理解为 8÷25=0.32。
答案:
下载量与下载时间的比是 3.2 : 10,
化成最简整数比是 8 : 25,
比值是 0.32。
(4)写出下面各杯糖和糖水的最简整数比,并回答问题。


1:6
2:5
1:3
1:4
答案:
1. 首先求各杯糖和糖水的比:
①号杯:
糖水质量$=$糖的质量$+$水的质量$=10 + 50=60$克。
糖和糖水的比为$10:60=\frac{10}{10}:\frac{60}{10}=1:6$(根据比的基本性质$a:b=(a÷ n):(b÷ n)$,$n\neq0$)。
②号杯:
糖水质量$=100 + 150 = 250$克。
糖和糖水的比为$100:250=\frac{100÷50}{250÷50}=2:5$。
③号杯:
糖水质量$=30 + 60 = 90$克。
糖和糖水的比为$30:90=\frac{30÷30}{90÷30}=1:3$。
④号杯:
糖水质量$=10+30 = 40$克。
糖和糖水的比为$10:40=\frac{10÷10}{40÷10}=1:4$。
2. 然后比较各杯糖水的浓度(浓度$=\frac{糖的质量}{糖水的质量}$):
①号杯浓度$=\frac{1}{6}\approx0.167$;
②号杯浓度$=\frac{2}{5}=0.4$;
③号杯浓度$=\frac{1}{3}\approx0.333$;
④号杯浓度$=\frac{1}{4}=0.25$。
所以各杯糖和糖水的最简整数比分别为$1:6$,$2:5$,$1:3$,$1:4$;②号杯中糖水最甜。
故答案依次为:$1:6$;$2:5$;$1:3$;$1:4$;②。
①号杯:
糖水质量$=$糖的质量$+$水的质量$=10 + 50=60$克。
糖和糖水的比为$10:60=\frac{10}{10}:\frac{60}{10}=1:6$(根据比的基本性质$a:b=(a÷ n):(b÷ n)$,$n\neq0$)。
②号杯:
糖水质量$=100 + 150 = 250$克。
糖和糖水的比为$100:250=\frac{100÷50}{250÷50}=2:5$。
③号杯:
糖水质量$=30 + 60 = 90$克。
糖和糖水的比为$30:90=\frac{30÷30}{90÷30}=1:3$。
④号杯:
糖水质量$=10+30 = 40$克。
糖和糖水的比为$10:40=\frac{10÷10}{40÷10}=1:4$。
2. 然后比较各杯糖水的浓度(浓度$=\frac{糖的质量}{糖水的质量}$):
①号杯浓度$=\frac{1}{6}\approx0.167$;
②号杯浓度$=\frac{2}{5}=0.4$;
③号杯浓度$=\frac{1}{3}\approx0.333$;
④号杯浓度$=\frac{1}{4}=0.25$。
所以各杯糖和糖水的最简整数比分别为$1:6$,$2:5$,$1:3$,$1:4$;②号杯中糖水最甜。
故答案依次为:$1:6$;$2:5$;$1:3$;$1:4$;②。
(5)做一批零件,王师傅 5 小时完成,李师傅 6 小时完成,王师傅和李师傅的工作效率比是(
6:5
)。
答案:
解析:本题考查工作效率、工作时间和工作总量之间的关系。
工作效率=工作总量$÷$工作时间,当工作总量一定时,工作效率与工作时间成反比。
王师傅$5$小时完成一批零件,李师傅$6$小时完成一批零件,把工作总量看成单位“$1$”,
王师傅的工作效率是$1÷5=\frac{1}{5}$,李师傅的工作效率是$1÷6=\frac{1}{6}$,
王师傅和李师傅的工作效率比是$\frac{1}{5}:\frac{1}{6}=6:5$。
答案:$6:5$。
工作效率=工作总量$÷$工作时间,当工作总量一定时,工作效率与工作时间成反比。
王师傅$5$小时完成一批零件,李师傅$6$小时完成一批零件,把工作总量看成单位“$1$”,
王师傅的工作效率是$1÷5=\frac{1}{5}$,李师傅的工作效率是$1÷6=\frac{1}{6}$,
王师傅和李师傅的工作效率比是$\frac{1}{5}:\frac{1}{6}=6:5$。
答案:$6:5$。
2. 化简比。
$42:56$
$1.25:2$
$\frac{4}{5}:5$
$2.5:\frac{3}{4}$
$42:56$
$1.25:2$
$\frac{4}{5}:5$
$2.5:\frac{3}{4}$
答案:
解析:本题考查的是化简比的知识点。化简比需要找到两个数的最大公约数,然后将两个数分别除以这个最大公约数,从而得到最简形式的比。对于包含分数的比,可以先将分数化为小数或者找到分数的最小公倍数,再进行化简。
答案:
42:56
=(42÷14):(56÷14)
=3:4
1.25:2
=(1.25×4):(2×4)
=5:8
$\frac{4}{5}:5$
=$(\frac{4}{5}×5):(5×5)$
=4:25
$2.5:\frac{3}{4}$
=$(2.5×4):(\frac{3}{4}×4)$
=10:3
答案:
42:56
=(42÷14):(56÷14)
=3:4
1.25:2
=(1.25×4):(2×4)
=5:8
$\frac{4}{5}:5$
=$(\frac{4}{5}×5):(5×5)$
=4:25
$2.5:\frac{3}{4}$
=$(2.5×4):(\frac{3}{4}×4)$
=10:3
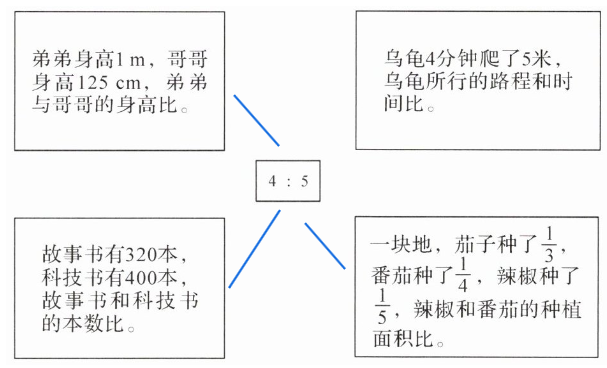
3. 下面情境中哪些可以用 $4:5$ 表示?用线连一连。


答案:

查看更多完整答案,请扫码查看


