1. 甲数的$\frac{5}{6}和乙数的\frac{4}{5}$相等(甲、乙两数均不等于0),那么甲数(
A.<
B.>
C.=
D.无法确定
A
)乙数。A.<
B.>
C.=
D.无法确定
答案:
解析:本题考查的是利用比例关系判断数的大小。
设甲数为a,乙数为b。
根据题目,有:
$\frac{5}{6}a = \frac{4}{5}b$,
为了比较a和b的大小,可以解这个方程,找出a和b的关系。
将方程两边同时乘以30(即6和5的最小公倍数)来消去分数:
$30 × \frac{5}{6}a = 30 × \frac{4}{5}b$,
$25a = 24b$,
$a = \frac{24}{25}b$。
由于$\frac{24}{25} \lt 1$,所以 $a \lt b$。
答案:A。
设甲数为a,乙数为b。
根据题目,有:
$\frac{5}{6}a = \frac{4}{5}b$,
为了比较a和b的大小,可以解这个方程,找出a和b的关系。
将方程两边同时乘以30(即6和5的最小公倍数)来消去分数:
$30 × \frac{5}{6}a = 30 × \frac{4}{5}b$,
$25a = 24b$,
$a = \frac{24}{25}b$。
由于$\frac{24}{25} \lt 1$,所以 $a \lt b$。
答案:A。
2. 两根同样长的绳子,第一根剪去它的$\frac{3}{8}$,第二根剪去$\frac{3}{8}$米,余下部分(
A.第一根长
B.第二根长
C.一样长
D.无法比较
D
)。A.第一根长
B.第二根长
C.一样长
D.无法比较
答案:
解析:本题考查的知识点是分数意义的理解及比较。
两根绳子原本长度相同,但剪去的长度方式不同:
第一根剪去的是它总长度的$\frac{3}{8}$,这是一个比例;
第二根剪去的是固定的$\frac{3}{8}$米,这是一个具体的长度。
由于不知道绳子的原始长度,因此无法准确计算出第一根绳子剪去的具体长度,也就无法直接比较两根绳子余下的部分哪根更长。
例如,如果绳子原长1米,那么第一根剪去$\frac{3}{8}$米,和第二根剪去的长度一样,余下部分也一样长;
但如果绳子原长大于1米,比如8米,那么第一根剪去的长度是3米,比第二根剪去的$\frac{3}{8}$米要长,所以第二根余下的部分就更长;
反之,如果绳子原长小于1米,比如$\frac{3}{8}$米,那么第一根剪去的长度就小于$\frac{3}{8}$米,第一根余下的部分就更长。
由于题目没有给出绳子的原始长度,所以我们无法确定哪根绳子余下的部分更长。
答案:D。
两根绳子原本长度相同,但剪去的长度方式不同:
第一根剪去的是它总长度的$\frac{3}{8}$,这是一个比例;
第二根剪去的是固定的$\frac{3}{8}$米,这是一个具体的长度。
由于不知道绳子的原始长度,因此无法准确计算出第一根绳子剪去的具体长度,也就无法直接比较两根绳子余下的部分哪根更长。
例如,如果绳子原长1米,那么第一根剪去$\frac{3}{8}$米,和第二根剪去的长度一样,余下部分也一样长;
但如果绳子原长大于1米,比如8米,那么第一根剪去的长度是3米,比第二根剪去的$\frac{3}{8}$米要长,所以第二根余下的部分就更长;
反之,如果绳子原长小于1米,比如$\frac{3}{8}$米,那么第一根剪去的长度就小于$\frac{3}{8}$米,第一根余下的部分就更长。
由于题目没有给出绳子的原始长度,所以我们无法确定哪根绳子余下的部分更长。
答案:D。
3. 下面各图中,能正确表示$\frac{2}{3}\text{m}^2$的是(

C
)。
答案:
解析:本题考查分数的意义。
A选项:将长方形平均分为3份,其中一份占$3m^2$的$\frac{1}{3}$,是$1m^2$,不合题意;
B选项:将长方形平均分为6份,其中一份占$3m^2$的$\frac{1}{6}$,是$0.5m^2$,不合题意;
C选项:将长方形平均分为3份,其中一份占$2m^2$的$\frac{1}{3}$,是$\frac{2}{3}m^2$,符合题意;
D选项:将长方形平均分为6份,其中一份占$3m^2$的$\frac{1}{6}$,是$0.5m^2$,不合题意。
答案:C。
A选项:将长方形平均分为3份,其中一份占$3m^2$的$\frac{1}{3}$,是$1m^2$,不合题意;
B选项:将长方形平均分为6份,其中一份占$3m^2$的$\frac{1}{6}$,是$0.5m^2$,不合题意;
C选项:将长方形平均分为3份,其中一份占$2m^2$的$\frac{1}{3}$,是$\frac{2}{3}m^2$,符合题意;
D选项:将长方形平均分为6份,其中一份占$3m^2$的$\frac{1}{6}$,是$0.5m^2$,不合题意。
答案:C。
4. 根据图示,求梨有多少筐的算式是(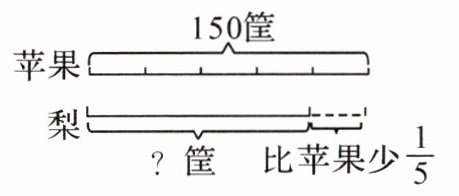
A.$150×\frac{1}{5}$
B.$150-\frac{1}{5}$
C.$150×(1+\frac{1}{5})$
D.$150×(1-\frac{1}{5})$
D
)。
A.$150×\frac{1}{5}$
B.$150-\frac{1}{5}$
C.$150×(1+\frac{1}{5})$
D.$150×(1-\frac{1}{5})$
答案:
解析:本题可根据线段图分析梨和苹果筐数的数量关系,进而得出求梨筐数的算式。
从线段图中可知,苹果有$150$筐,梨比苹果少$\frac{1}{5}$,这里是把苹果的筐数看作单位“$1$”,那么梨的筐数是苹果的$1 - \frac{1}{5}$。
根据求一个数的几分之几是多少用乘法计算,所以求梨的筐数的算式为$150×(1 - \frac{1}{5})$。
答案:D。
从线段图中可知,苹果有$150$筐,梨比苹果少$\frac{1}{5}$,这里是把苹果的筐数看作单位“$1$”,那么梨的筐数是苹果的$1 - \frac{1}{5}$。
根据求一个数的几分之几是多少用乘法计算,所以求梨的筐数的算式为$150×(1 - \frac{1}{5})$。
答案:D。
5. 比9吨少$\frac{1}{3}$是(
6
)吨,比90吨多$\frac{1}{3}$吨是(90$\frac{1}{3}$
)吨。
答案:
解析:
本题考查的是分数的运算。
比9吨少$\frac{1}{3}$,则减少的部分是9吨的$\frac{1}{3}$,即3吨。
所以,比9吨少$\frac{1}{3}$的重量是:
9 - 3 = 6(吨)。
比90吨多$\frac{1}{3}$吨,则直接在90吨的基础上加上$\frac{1}{3}$吨,
即:90 + $\frac{1}{3}$ = 90$\frac{1}{3}$(吨)。
也可以转化为小数:90 + 0.333... ≈ 90.333(吨)。
但按照题目要求,这里保留分数形式更为精确,所以答案是90$\frac{1}{3}$吨。
答案:6吨;90$\frac{1}{3}$吨。
本题考查的是分数的运算。
比9吨少$\frac{1}{3}$,则减少的部分是9吨的$\frac{1}{3}$,即3吨。
所以,比9吨少$\frac{1}{3}$的重量是:
9 - 3 = 6(吨)。
比90吨多$\frac{1}{3}$吨,则直接在90吨的基础上加上$\frac{1}{3}$吨,
即:90 + $\frac{1}{3}$ = 90$\frac{1}{3}$(吨)。
也可以转化为小数:90 + 0.333... ≈ 90.333(吨)。
但按照题目要求,这里保留分数形式更为精确,所以答案是90$\frac{1}{3}$吨。
答案:6吨;90$\frac{1}{3}$吨。
6. 学校进行视力检测。六年级共有240人,检测结果中近视的人数是总人数的$\frac{1}{3}$。近视的学生中,男生占$\frac{5}{8}$,近视的男生有几人?
答案:
240×$\frac{1}{3}$=80(人)
80×$\frac{5}{8}$=50(人)
答:近视的男生有50人。
80×$\frac{5}{8}$=50(人)
答:近视的男生有50人。
7. 王叔叔开车从甲地出发,如果速度是90千米/时,那么6小时到达乙地。如果速度提高$\frac{1}{5}$,那么几小时可以到达乙地?

答案:
解析:本题考查路程、速度和时间之间的关系。
根据$路程 = 速度× 时间$,已知速度是$90$千米/时,时间是$6$小时,可得甲乙两地的距离为:
$90× 6 = 540$(千米)
速度提高$\frac{1}{5}$,那么提高后的速度为:
$90 + 90× \frac{1}{5}= 90 + 18 = 108$(千米/时)
再根据$时间 = 路程÷ 速度$,可得提高速度后到达乙地所需的时间为:
$540÷ 108 = 5$(小时)
答案:5小时。
根据$路程 = 速度× 时间$,已知速度是$90$千米/时,时间是$6$小时,可得甲乙两地的距离为:
$90× 6 = 540$(千米)
速度提高$\frac{1}{5}$,那么提高后的速度为:
$90 + 90× \frac{1}{5}= 90 + 18 = 108$(千米/时)
再根据$时间 = 路程÷ 速度$,可得提高速度后到达乙地所需的时间为:
$540÷ 108 = 5$(小时)
答案:5小时。
查看更多完整答案,请扫码查看


