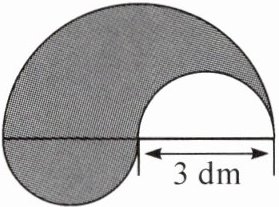
1. 计算下面各图阴影部分的周长和面积。



答案:
图1:3.14×3+3.14×3×2÷2=18.84( dm)
3.14×3²÷2=14.13( dm²)
图2:6+2+2=10(cm)
3.14×10÷2+3.14×6÷2+2×2=29.12( cm)
3.14×(10÷2)²÷2-3.14×(6÷2)²÷2=25.12( cm²)
(1)将一个圆平均分成 200 个完全相同的小扇形,拼成的近似长方形的周长比原来圆的周长多 10 cm。这个圆的面积是(
A.78.5
B.89.5
C.314
D.62.8
A
)$\text{cm}^2$。A.78.5
B.89.5
C.314
D.62.8
答案:
解析:本题主要考查圆的面积公式的推导过程。
将一个圆平均分成若干个完全相同的小扇形后,拼成的近似长方形的周长比原来圆的周长多了两条半径的长度。
已知拼成的近似长方形的周长比原来圆的周长多$10cm$,即圆的半径为:$10 ÷ 2=5(cm)$。
根据圆的面积公式$S = \pi r^{2}$,其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$表示圆的半径,可得:
$S=3.14 × 5^{2}$
$=3.14 × 25$
$=78.5(cm^{2})$。
答案:A。
将一个圆平均分成若干个完全相同的小扇形后,拼成的近似长方形的周长比原来圆的周长多了两条半径的长度。
已知拼成的近似长方形的周长比原来圆的周长多$10cm$,即圆的半径为:$10 ÷ 2=5(cm)$。
根据圆的面积公式$S = \pi r^{2}$,其中$S$表示圆的面积,$\pi$通常取$3.14$,$r$表示圆的半径,可得:
$S=3.14 × 5^{2}$
$=3.14 × 25$
$=78.5(cm^{2})$。
答案:A。
(2)一个圆的半径增加 1 cm,那么它的面积增加(
A.3.14 $\text{cm}^2$
B.1 $\text{cm}^2$
C.6.28 $\text{cm}^2$
D.无法确定
D
)。A.3.14 $\text{cm}^2$
B.1 $\text{cm}^2$
C.6.28 $\text{cm}^2$
D.无法确定
答案:
解析:
本题考查圆的面积计算。
首先,需要知道圆的面积公式是$S = \pi r^2$,其中$r$是圆的半径。
现在,题目说圆的半径增加了1cm,需要找出面积增加了多少。
假设原来的半径是$r$ cm,那么原来的面积就是 $\pi r^2$ $cm^2$。
半径增加1cm后,新的半径是 $r + 1$ cm,所以新的面积是 $\pi (r + 1)^2$ $cm^2$。
那么,面积的增加量就是新的面积减去原来的面积,即:
$\pi (r + 1)^2 - \pi r^2$
$= \pi (r^2 + 2r + 1) - \pi r^2$
$= \pi r^2 + 2\pi r + \pi - \pi r^2$
$= 2\pi r + \pi$
由于$\pi$取3.14,且$r$是一个未知数,所以无法确定面积具体增加了多少,因为增加的面积还取决于原来的半径$r$。
由于题目没有给出具体的半径值,所以无法计算出面积具体增加了多少。因此,答案是D.无法确定。
答案:D。
本题考查圆的面积计算。
首先,需要知道圆的面积公式是$S = \pi r^2$,其中$r$是圆的半径。
现在,题目说圆的半径增加了1cm,需要找出面积增加了多少。
假设原来的半径是$r$ cm,那么原来的面积就是 $\pi r^2$ $cm^2$。
半径增加1cm后,新的半径是 $r + 1$ cm,所以新的面积是 $\pi (r + 1)^2$ $cm^2$。
那么,面积的增加量就是新的面积减去原来的面积,即:
$\pi (r + 1)^2 - \pi r^2$
$= \pi (r^2 + 2r + 1) - \pi r^2$
$= \pi r^2 + 2\pi r + \pi - \pi r^2$
$= 2\pi r + \pi$
由于$\pi$取3.14,且$r$是一个未知数,所以无法确定面积具体增加了多少,因为增加的面积还取决于原来的半径$r$。
由于题目没有给出具体的半径值,所以无法计算出面积具体增加了多少。因此,答案是D.无法确定。
答案:D。
(3)下列各图中大正方形边长都是 10 cm,涂色部分的面积可以用算式$10^{2}-3.14×5^{2}$计算的个数是(
A.2
B.3
C.4
D.5
D
)。A.2
B.3
C.4
D.5
答案:
1. 图1:大正方形面积$10^2$,空白为直径10cm的圆,面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
2. 图2:空白为2个直径10cm的半圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
3. 图3:空白为1个直径10cm的半圆和1个半径5cm的半圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
4. 图4:空白为半径10cm的$\frac{1}{4}$圆,面积$\frac{1}{4}×3.14×10^2 = 3.14×25$,涂色面积$10^2 - 3.14×25 = 10^2 - 3.14×5^2$,符合。
5. 图5:空白为4个半径5cm的$\frac{1}{4}$圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
答案:D
2. 图2:空白为2个直径10cm的半圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
3. 图3:空白为1个直径10cm的半圆和1个半径5cm的半圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
4. 图4:空白为半径10cm的$\frac{1}{4}$圆,面积$\frac{1}{4}×3.14×10^2 = 3.14×25$,涂色面积$10^2 - 3.14×25 = 10^2 - 3.14×5^2$,符合。
5. 图5:空白为4个半径5cm的$\frac{1}{4}$圆(合为1个整圆),面积$3.14×5^2$,涂色面积$10^2 - 3.14×5^2$,符合。
答案:D
3. 如图,运动场两端是半圆形,中间是长方形。绕着运动场跑一圈是多少米?现在打算给运动场中间的长方形场地铺草皮,需要草皮多少平方米?


答案:
3.14×70+(160-70)×2=399.8(米)
(160-70)×70+(70÷2)²×3.14=10146.5(平方米)
(160-70)×70+(70÷2)²×3.14=10146.5(平方米)
4. 人民广场有一个周长是 43.96 m 的圆形喷水池,外有一条 3 m 宽的小路围着喷水池。这条小路的面积是多少平方米?
答案:
解析:
本题考查圆的周长和面积的计算,以及圆环面积的计算。
首先需要根据喷水池的周长计算出喷水池的半径,然后再算出包括小路在内的大圆的半径,最后通过计算两个圆的面积差来得到小路的面积。
圆的周长公式为$C = 2\pi r$,由此可以计算出喷水池的半径$r$。
圆的面积公式为$S = \pi r^{2}$,由此可以分别计算出喷水池的面积和包括小路在内的大圆的面积。
最后,小路的面积就是大圆的面积减去喷水池的面积。
答案:
喷水池的半径:
$43.96 ÷ (2× 3.14) = 7$(m),
大圆的半径:
$7 + 3 = 10$(m),
喷水池的面积:
$3.14 × 7^{2} = 153.86$($m^2$),
大圆的面积:
$3.14 × 10^{2} = 314$($m^2$),
小路的面积:
$314 - 153.86 = 160.14$($m^2$),
所以,这条小路的面积是$160.14$平方米。
本题考查圆的周长和面积的计算,以及圆环面积的计算。
首先需要根据喷水池的周长计算出喷水池的半径,然后再算出包括小路在内的大圆的半径,最后通过计算两个圆的面积差来得到小路的面积。
圆的周长公式为$C = 2\pi r$,由此可以计算出喷水池的半径$r$。
圆的面积公式为$S = \pi r^{2}$,由此可以分别计算出喷水池的面积和包括小路在内的大圆的面积。
最后,小路的面积就是大圆的面积减去喷水池的面积。
答案:
喷水池的半径:
$43.96 ÷ (2× 3.14) = 7$(m),
大圆的半径:
$7 + 3 = 10$(m),
喷水池的面积:
$3.14 × 7^{2} = 153.86$($m^2$),
大圆的面积:
$3.14 × 10^{2} = 314$($m^2$),
小路的面积:
$314 - 153.86 = 160.14$($m^2$),
所以,这条小路的面积是$160.14$平方米。
查看更多完整答案,请扫码查看


