《2025年新课标学习方法指导丛书六年级数学上册人教版》

(1)用圆规画圆时,针尖所在的点叫作圆心,决定圆的位置；连接圆心和圆上任意一点的线段叫作半径,决定圆的大小；通过圆心并且两端都在圆上的线段叫作直径。

答案： 解析：题目考查圆的基础定义和性质，涉及到圆心、半径和直径的概念。
答案：用圆规画圆时,针尖所在的点叫作(圆心)，决定圆的(位置)；连接圆心和圆上任意一点的线段叫作(半径)，决定圆的(大小)；通过圆心并且两端都在圆上的线段叫作(直径)。

(2)在同一个圆里,所有的半径都相等,所有的直径都相等；直径与半径的最简整数比是2:1。

答案： 解析：本题考查圆的基本性质，包括半径和直径的关系以及它们在同一个圆中的特性。在同一个圆中，所有的半径长度相等，所有的直径长度也相等。直径是半径的两倍，所以直径与半径的比是2:1。
答案：在同一个圆里，所有的半径都相等，所有的直径都相等；直径与半径的最简整数比是2:1。

(3)圆规两脚之间的距离是4 cm,这时画出的圆的直径是(8)cm。

答案： 解析：圆规两脚之间的距离是圆的半径。已知半径为4 cm，根据圆的性质，直径是半径的两倍。因此，直径 $d = 2 × r$。
答案：8 cm。

2. 用圆规画圆。
$ r= 2\ \text{cm} $
$ d= 60\ \text{mm} $

答案： 解析：本题是实践题，考查圆规画圆的方法。题目给出了半径 $r= 2 \text{cm}$ 和直径 $d= 60 \text{mm}$，但这两个数据是矛盾的，因为 $60 \text{mm} = 6 \text{cm}$，直径应该是半径的两倍，但这里给出的直径是半径的三倍。由于这是实践题，我们只需按照给定的半径（或转换后的直径）来画圆。
答案：图略（用圆规，首先确定圆心，将圆规的一脚固定在圆心上，调整圆规两脚之间的距离至2cm（或根据直径6cm调整至一半即3cm作为半径），然后旋转圆规，即可画出一个圆）。

3. 看图填空。

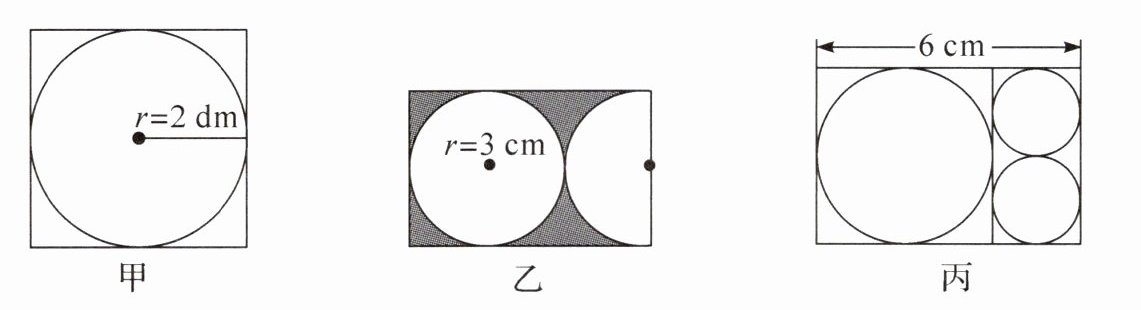
(1)如图甲,正方形的边长是(4)dm,正方形的周长是(16)dm。
(2)如图乙,圆的直径是(6)cm,长方形的周长是(30)cm。
(3)如图丙,长方形的纸剪出两个相同的圆后,剩下部分正好是个正方形。原来长方形的面积是(24)$cm^2$。

答案：
(1)4，16
(2)6，30
(3)24