11. 将二次函数 $ y = x ^ { 2 } - 4 x + 5 $ 化成 $ y = a ( x - h ) ^ { 2 } + k $ 的形式为______。
答案:
y=(x - 2)² + 1
12. 经过 $ A ( 4, 0 ) $, $ B ( - 2, 0 ) $, $ C ( 0, 3 ) $ 三点的抛物线的函数解析式是______。
答案:
y = -$\frac{3}{8}$x² + $\frac{3}{4}$x + 3
13. 已知点 $ A ( a ^ { 2 }, y _ { 1 } ) $, $ B ( a ^ { 2 } + 1, y _ { 2 } ) $, $ C ( a ^ { 2 } + 3, y _ { 3 } ) $ 都在函数 $ y = - ( x + 4 ) ^ { 2 } $ 的图象上,则 $ y _ { 1 } $, $ y _ { 2 } $, $ y _ { 3 } $ 的大小关系是______。(用“ $ > $ ”连接)
答案:
y₁>y₂>y₃
14. 如图,正方形的边长为4,以正方形的中心为原点建立平面直角坐标系,作出函数 $ y = \frac { 1 } { 3 } x ^ { 2 } $ 与 $ y = - \frac { 1 } { 3 } x ^ { 2 } $ 的图象,则阴影部分的面积是______。
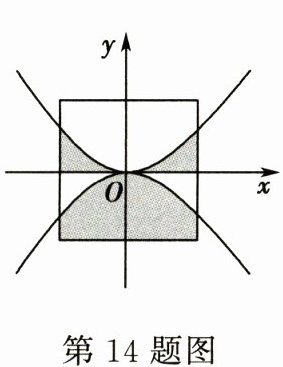

答案:
8
15. 已知二次函数 $ y = a x ^ { 2 } + b x + 4 $ 的图象如图,则关于 $ x $ 的方程 $ a x ^ { 2 } + b x = 0 $ 的根为______。
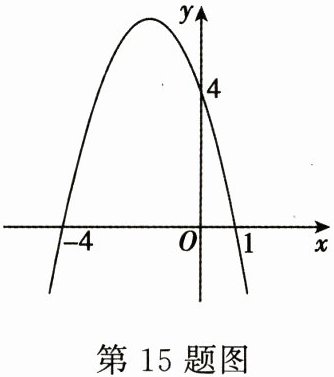

答案:
x₁ = 0,x₂ = -3
16. 某农场拟建两间矩形饲养室,一面靠现有墙(墙足够长),中间用一道墙隔开,并在如图的三处各留1m宽的门。已知计划中的材料可建墙体(不包括门)的总长为27m,则能建成的饲养室的面积最大为______ $ m ^ { 2 } $。


答案:
75
17. (6分)已知二次函数的解析式是 $ y = x ^ { 2 } - 2 x - 3 $。
(1)求该函数图象与 $ x $ 轴、 $ y $ 轴的交点坐标以及它的顶点坐标;
(2)根据(1)的结果在平面直角坐标系中利用描点法画出此抛物线。
(1)求该函数图象与 $ x $ 轴、 $ y $ 轴的交点坐标以及它的顶点坐标;
(2)根据(1)的结果在平面直角坐标系中利用描点法画出此抛物线。

答案:
解:
(1)令y = 0,则x² - 2x - 3 = 0,解得x₁ = -1,x₂ = 3.令x = 0,则y = -3.
∴抛物线y = x² - 2x - 3与x轴交点的坐标为(-1,0),(3,0),与y轴交点的坐标为(0,-3).由y = x² - 2x - 3 = (x - 1)² - 4,可得其顶点坐标为(1,-4).
(2)列表如下:x … -1 0 1 2 3 …y … 0 -3 -4 -3 0 …画出抛物线如图.
解:
(1)令y = 0,则x² - 2x - 3 = 0,解得x₁ = -1,x₂ = 3.令x = 0,则y = -3.
∴抛物线y = x² - 2x - 3与x轴交点的坐标为(-1,0),(3,0),与y轴交点的坐标为(0,-3).由y = x² - 2x - 3 = (x - 1)² - 4,可得其顶点坐标为(1,-4).
(2)列表如下:x … -1 0 1 2 3 …y … 0 -3 -4 -3 0 …画出抛物线如图.

查看更多完整答案,请扫码查看


