《2025年初中同步练习册分层卷九年级数学上册人教版》

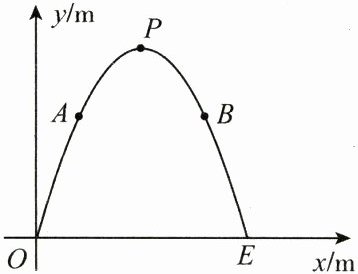
8. (12 分)现要修建一条隧道, 其截面为抛物线形, 如图所示, 线段 $ OE $ 表示水平的路面, 以 $ O $ 为坐标原点, 以 $ OE $ 所在直线为 $ x $ 轴, 以过点 $ O $ 且垂直于 $ x $ 轴的直线为 $ y $ 轴, 建立平面直角坐标系.根据设计要求: $ OE= 10 \mathrm{~m} $, 该抛物线的顶点 $ P $ 到 $ OE $ 的距离为 $ 9 \mathrm{~m} $.
(1)求满足设计要求的抛物线的函数解析式;
(2)如图, 现需在这一隧道内壁的点 $ A, B $ 处分别安装照明灯.已知点 $ A, B $ 到 $ OE $ 的距离均为 $ 6 \mathrm{~m} $, 求点 $ A, B $ 的坐标.

答案： 解：
(1)由题意，得抛物线的顶点为P(5，9)，
∴设抛物线的函数解析式为y=a(x-5)²+9.
把(0，0)代入，得a=-$\frac{9}{25}$，
∴抛物线的函数解析式为y=-$\frac{9}{25}$(x-5)²+9.
(2)令y=6，得-$\frac{9}{25}$(x-5)²+9=6，
解得x₁=5+$\frac{5\sqrt{3}}{3}$，x₂=5-$\frac{5\sqrt{3}}{3}$.
∴A(5-$\frac{5\sqrt{3}}{3}$，6)，B(5+$\frac{5\sqrt{3}}{3}$，6).

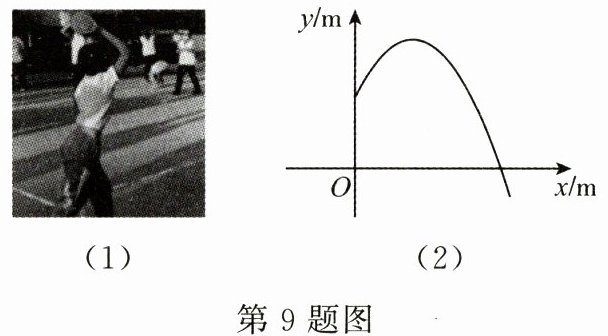
9. (4 分)如图(1), 校运动会上, 九年级的同学们进行了投实心球比赛.我们发现, 实心球在空中飞行的轨迹可以近似看作是抛物线.如图(2)建立平面直角坐标系, 已知实心球运动的高度 $ y(\mathrm{~m}) $ 与水平距离 $ x(\mathrm{~m}) $ 之间的函数关系是 $ y= -\frac{1}{12} x^{2}+\frac{2}{3} x+\frac{5}{3} $, 则该同学此次投掷实心球的成绩是 ( )

[A] 2 m
[B] 6 m
[C] 8 m
[D] 10 m

答案： D

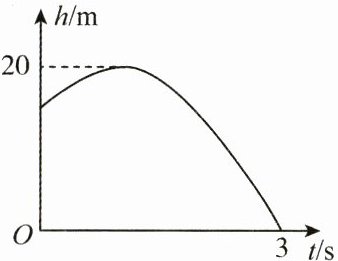
10. (4 分)距离地面有一定高度的某发射装置竖直向上发射物体, 物体离地面的高度 $ h(\mathrm{~m}) $ 与物体运动的时间 $ t(\mathrm{~s}) $ 之间满足函数关系 $ h= -5 t^{2}+m t+n $, 其图象如图所示, 物体运动的最高点离地面 $ 20 \mathrm{~m} $, 物体从发射到落地的运动时间为 $ 3 \mathrm{~s} $.设 $ w $ 表示 $ 0 \mathrm{~s} $ 到 $ t \mathrm{~s} $ 时 $ h $ 的值的 “极差” (即 $ 0 \mathrm{~s} $ 到 $ t \mathrm{~s} $ 时 $ h $ 的最大值与最小值的差), 则当 $ 0 \leqslant t \leqslant 1 $ 时, $ w $ 的取值范围是______; 当 $ 2 \leqslant t \leqslant 3 $ 时, $ w $ 的取值范围是______.

答案： 0≤w≤5 5≤w≤20