《2025年初中同步练习册分层卷九年级数学上册人教版》

17. (8 分)如图,$ AB $ 是 $ \odot O $ 的直径,$ CD $ 是 $ \odot O $ 的一条弦,且 $ CD \perp AB $ 于点 $ E $.
(1)求证：$ \angle BCO = \angle D $；
(2)若 $ CD = 4\sqrt{2} $,$ AE = 2 $,求 $ \odot O $ 的半径.

答案：
(1)证明：
∵OC=OB，
∴∠BCO=∠B.
∵∠B=∠D，
∴∠BCO=∠D.
(2)解：
∵AB是⊙O的直径，且CD⊥AB于点E，
∴CE=$\frac{1}{2}$CD=$\frac{1}{2}$×4$\sqrt{2}$=2$\sqrt{2}$.在Rt△OCE中，OC²=CE²+OE².设⊙O的半径为r，则OC=r，OE=OA－AE=r－2，
∴r²=(2$\sqrt{2}$)²+(r－2)²，解得r=3.
∴⊙O的半径为3.

18. (8 分)如图,残破的圆形轮片上,弦 $ AB $ 的垂直平分线交 $ \overset{\frown}{AB} $ 于点 $ C $,交弦 $ AB $ 于点 $ D $.已知 $ AB = 24 cm $,$ CD = 8 cm $.
(1)作出此残片所在的圆；(不写作法,保留作图痕迹)
(2)求残片所在圆的面积.

答案：

(1)如图，连接AC，作弦AC的垂直平分线，与弦AB的垂直平分线交于点O，以点O为圆心、OA长为半径作⊙O，⊙O就是此残片所在的圆.
(2)如图，连接OA.设OA=x cm，则OD=(x－8)cm.在Rt△AOD中，AD=$\frac{1}{2}$AB=12 cm.根据勾股定理列方程，得x²=12²+(x－8)²，解得x=13，即圆的半径为13 cm.
∴圆的面积为π×13²=169π(cm²).

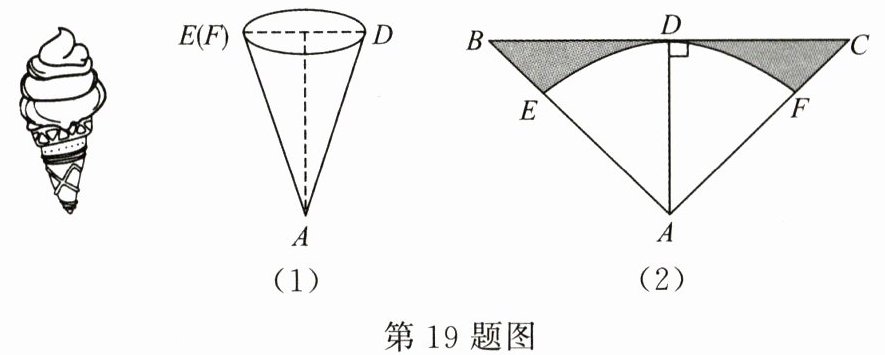
19. (8 分)某种冰激凌的外包装可以视为圆锥,如图(1),它的底面圆的直径 $ DE $ 与母线 $ AD $ 长度之比为 $ 1:2 $.制作这种外包装需要用如图(2)所示的等腰三角形材料,其中 $ AB = AC $,$ AD \perp BC $.将扇形 $ EAF $ 围成圆锥时,$ AE $,$ AF $ 恰好重合.
(1)求这种加工材料的顶角 $ \angle BAC $ 的大小；
(2)若圆锥底面圆的直径 $ DE $ 为 $ 5 cm $,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 $ \pi $)

答案：
(1)设∠BAC=n°.由题意，得π·DE=$\frac{nπ·AD}{180}$，AD=2DE，
∴n=90.
∴∠BAC=90°.
(2)由
(1)得∠BAC=90°.又
∵AB=AC，AD⊥BC，
∴D为BC的中点.
∴BC=2AD.
∵AD=2DE=10 cm，
∴BC=2AD=20 cm.
∴S阴影=$\frac{1}{2}$BC·AD－S扇形AEF=$\frac{1}{2}$×20×10－$\frac{90π×10²}{360}$=(100－25π)cm².