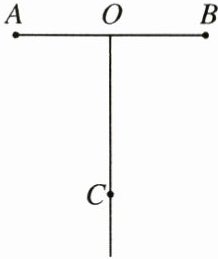
21. (12 分)如图,$AO = OB = 50\ cm$,$OC$是一条射线,$OC\perp AB$,一只蚂蚁由点$A以2\ cm/s的速度向点B$爬行,同时另一只蚂蚁由点$O以3\ cm/s的速度沿OC$方向爬行.多长时间时,两只蚂蚁与点$O组成的三角形的面积为450\ cm^{2}$?

答案:
解:分两种情况进行讨论:
①如图
(1),当一只蚂蚁在AO上运动时,设$x\ s$时两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
由题意,得$\frac{1}{2}×3x\cdot(50 - 2x)=450$.
整理,得$x^{2}-25x + 150 = 0$,
解得$x_{1}=15$,$x_{2}=10$.

②如图
(2),当一只蚂蚁在OB上运动时,设$y\ s$时,两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
由题意,得$\frac{1}{2}×3y\cdot(2y - 50)=450$.
整理,得$y^{2}-25y - 150 = 0$,
解得$y_{1}=30$,$y_{2}=-5$(不符合题意,舍去).综上,10 s或15 s或30 s时,两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
解:分两种情况进行讨论:
①如图
(1),当一只蚂蚁在AO上运动时,设$x\ s$时两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
由题意,得$\frac{1}{2}×3x\cdot(50 - 2x)=450$.
整理,得$x^{2}-25x + 150 = 0$,
解得$x_{1}=15$,$x_{2}=10$.

②如图
(2),当一只蚂蚁在OB上运动时,设$y\ s$时,两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
由题意,得$\frac{1}{2}×3y\cdot(2y - 50)=450$.
整理,得$y^{2}-25y - 150 = 0$,
解得$y_{1}=30$,$y_{2}=-5$(不符合题意,舍去).综上,10 s或15 s或30 s时,两只蚂蚁与点O组成的三角形的面积为$450\ cm^{2}$.
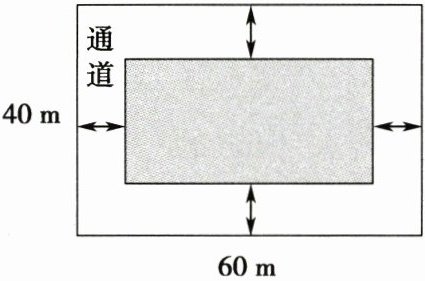
22. (12 分)如图,为了美化环境,某小区计划在一块矩形空地上修建一个面积为$1500\ m^{2}$的矩形草坪,并将草坪四周余下的空地修建成同样宽的通道,已知矩形空地的长为$60\ m$,宽为$40\ m$.
(1)求通道的宽度;
(2)某公司承揽了该小区草坪的种植工程,计划种植“四季青”和“黑麦草”两种绿植,该公司种植“四季青”的单价是每平方米 30 元,超过$50\ m^{2}$后,每多出$5\ m^{2}$,所有“四季青”的种植单价可降低 1 元,但单价不低于每平方米 20 元.已知小区种植“四季青”的面积超过了$50\ m^{2}$,支付该公司种植“四季青”的费用为 2 000 元,求种植“四季青”的面积.
(1)求通道的宽度;
(2)某公司承揽了该小区草坪的种植工程,计划种植“四季青”和“黑麦草”两种绿植,该公司种植“四季青”的单价是每平方米 30 元,超过$50\ m^{2}$后,每多出$5\ m^{2}$,所有“四季青”的种植单价可降低 1 元,但单价不低于每平方米 20 元.已知小区种植“四季青”的面积超过了$50\ m^{2}$,支付该公司种植“四季青”的费用为 2 000 元,求种植“四季青”的面积.

答案:
解:
(1)设通道的宽度为$x\ m$.
由题意,得$(60 - 2x)(40 - 2x)=1500$,
解得$x_{1}=5$,$x_{2}=45$(不符合题意,舍去).
$\therefore$通道的宽度为5 m.
(2)设种植“四季青”的面积为$y\ m^{2}$.
由题意,得$y(30-\frac{y - 50}{5})=2000$,
解得$y_{1}=y_{2}=100$.
$\therefore$种植“四季青”的面积为$100\ m^{2}$.
(1)设通道的宽度为$x\ m$.
由题意,得$(60 - 2x)(40 - 2x)=1500$,
解得$x_{1}=5$,$x_{2}=45$(不符合题意,舍去).
$\therefore$通道的宽度为5 m.
(2)设种植“四季青”的面积为$y\ m^{2}$.
由题意,得$y(30-\frac{y - 50}{5})=2000$,
解得$y_{1}=y_{2}=100$.
$\therefore$种植“四季青”的面积为$100\ m^{2}$.
查看更多完整答案,请扫码查看


