《2025年初中同步练习册分层卷九年级数学上册人教版》

20. (10 分)如图, 在矩形 $ ABCD $ 中, 对角线 $ AC $ 的中点为 $ O $,点 $ G $, $ H $ 在对角线 $ AC $ 上, $ AG = CH $, 直线 $ GH $ 绕点 $ O $ 逆时针旋转 $ \alpha $, 与边 $ AB $, $ CD $ 分别相交于点 $ E $, $ F $ (点 $ E $ 不与点 $ A $, $ B $ 重合).
(1) 求证: 四边形 $ EHFG $ 是平行四边形;
(2) 若 $ \alpha = 90° $, $ AB = 9 $, $ AD = 3 $, 求 $ AE $ 的长.

| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | +0.5 |

答案：

(1)证明：
∵对角线$AC$的中点为$O$，
∴$AO = CO$。
∵$AG = CH$，
∴$GO = HO$。
∵四边形$ABCD$是矩形，
∴$AB// CD$。
∴$\angle DCA = \angle CAB$。
又
∵$CO = AO$，$\angle FOC = \angle EOA$。
∴$\triangle COF\cong\triangle AOE(ASA)$。
∴$FO = EO$。
又
∵$GO = HO$，
∴四边形$EHFG$是平行四边形。
(2)解：如图，连接$CE$。

∵$\alpha = 90^{\circ}$，
∴$EF\perp AC$。
∵$AO = CO$，
∴$EF$是$AC$的垂直平分线。
∴$AE = CE$。
在$Rt\triangle BCE$中，$CE^2 = BC^2 + BE^2$，
即$AE^2 = 9 + (9 - AE)^2$，解得$AE = 5$。

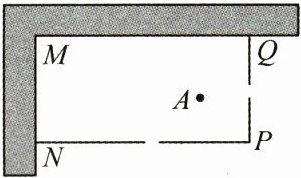
21. (12 分)某农场准备利用如图所示的直角墙角(两边足够长),用 $ 60 \, m $ 长的篱笆围成一个矩形家禽养殖场 $ MNPQ $ (篱笆只围 $ PQ $, $ PN $ 两边), 并在 $ PQ $, $ PN $ 两边上各开一个 $ 1 \, m $ 宽的门, 设 $ PQ = x \, m $, 养殖场的面积为 $ S \, m^2 $.
(1) 求 $ S $ 关于 $ x $ 的函数解析式.
(2) 求 $ S $ 的最大值.
(3) 若在直角墙角内的 $ A $ 处有一个水池, 且与墙 $ MQ $, $ MN $ 的距离分别是 $ 10 \, m $, $ 20 \, m $, 要将这个水池围在矩形养殖场内(含边界, 不考虑水池的尺寸), 则养殖场的面积能否为 $ 600 \, m^2 $? 若能, 求出 $ x $ 的值; 若不能, 请说明理由.

| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | +0.5 |

答案：
(1)依题意，得$PN = 60 - (x - 1) + 1 = (62 - x)m$，
∴$S = x(62 - x) = -x^2 + 62x$，
∴$S$关于$x$的函数解析式为$S = -x^2 + 62x$。
(2)$S = -x^2 + 62x = -(x - 31)^2 + 961$。
∵$a = -1 ＜ 0$，
∴当$x = 31$时，$S$最大，$S$的最大值为$961$。
(3)能。若养殖场的面积为$600m^2$，
则$-x^2 + 62x = 600$，
解得$x_1 = 12$，$x_2 = 50$。
根据题意，易知$x\geq10$，且$62 - x\geq20$，
∴$10\leq x\leq42$。
∴当$x = 12$时，养殖场的面积为$600m^2$。