22. (12 分)小李在景区销售一种旅游纪念品, 已知每件进价为 $ 6 $ 元, 当销售单价定为 $ 8 $ 元时, 每天可以销售 $ 200 $ 件.市场调查反映: 销售单价每提高 $ 1 $ 元, 日销量将会减少 $ 10 $ 件.物价部门规定: 销售单价不能超过 $ 12 $ 元.设该纪念品的销售单价为 $ x $ (单位: 元), 日销量为 $ y $ (单位: 件), 日销售利润为 $ w $ (单位: 元).
(1) 求 $ y $ 关于 $ x $ 的函数解析式.
(2) 要使日销售利润为 $ 720 $ 元, 销售单价应定为多少元?
(3) 求 $ w $ 关于 $ x $ 的函数解析式.当 $ x $ 为何值时, 日销售利润最大? 请求出最大利润.
| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | +0.5 |
(1) 求 $ y $ 关于 $ x $ 的函数解析式.
(2) 要使日销售利润为 $ 720 $ 元, 销售单价应定为多少元?
(3) 求 $ w $ 关于 $ x $ 的函数解析式.当 $ x $ 为何值时, 日销售利润最大? 请求出最大利润.
| 1 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | +0.5 |
答案:
(1)根据题意,得$y = 200 - 10(x - 8) = -10x + 280$。
故$y$关于$x$的函数解析式为$y = -10x + 280$。
(2)根据题意,得$w = (x - 6)(-10x + 280)=720$,
解得$x_1 = 10$,$x_2 = 24$(不符合题意,舍去)。
∴要使日销售利润为$720$元,销售单价应定为$10$元。
(3)根据题意,得$w = (x - 6)(-10x + 280)= -10(x - 17)^2 + 1210$。
∵$-10 < 0$,
∴当$x < 17$时,$w$随$x$的增大而增大。
∴当$x = 12$时,日销售利润最大,$w_{最大}= 960$。
故$w$关于$x$的函数解析式为$w = -10(x - 17)^2 + 1210$;
当$x$为$12$时,日销售利润最大,最大利润为$960$元。
(1)根据题意,得$y = 200 - 10(x - 8) = -10x + 280$。
故$y$关于$x$的函数解析式为$y = -10x + 280$。
(2)根据题意,得$w = (x - 6)(-10x + 280)=720$,
解得$x_1 = 10$,$x_2 = 24$(不符合题意,舍去)。
∴要使日销售利润为$720$元,销售单价应定为$10$元。
(3)根据题意,得$w = (x - 6)(-10x + 280)= -10(x - 17)^2 + 1210$。
∵$-10 < 0$,
∴当$x < 17$时,$w$随$x$的增大而增大。
∴当$x = 12$时,日销售利润最大,$w_{最大}= 960$。
故$w$关于$x$的函数解析式为$w = -10(x - 17)^2 + 1210$;
当$x$为$12$时,日销售利润最大,最大利润为$960$元。
23. (14 分)如图, 已知抛物线经过 $ A(-3, 0) $, $ B(0, 3) $ 两点,且其对称轴为直线 $ x = -1 $.
(1) 求此抛物线的函数解析式;
(2) 若点 $ P $ 是抛物线上点 $ A $ 与点 $ B $ 之间的动点(不包括点 $ A $, $ B $), 求 $ \triangle PAB $ 的面积的最大值, 并求出此时点 $ P $ 的坐标.
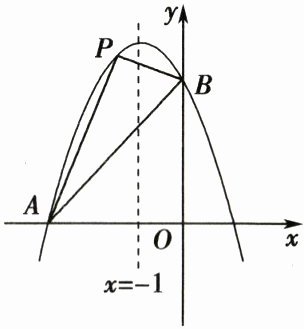
(1) 求此抛物线的函数解析式;
(2) 若点 $ P $ 是抛物线上点 $ A $ 与点 $ B $ 之间的动点(不包括点 $ A $, $ B $), 求 $ \triangle PAB $ 的面积的最大值, 并求出此时点 $ P $ 的坐标.

答案:
(1)
∵抛物线的对称轴是直线$x = -1$且经过点$A(-3, 0)$,
∴由抛物线的对称性可知抛物线还经过点$(1, 0)$。
设抛物线的函数解析式为$y = a(x - 1)(x + 3)$。
把$B(0, 3)$代入,得$3 = -3a$,
∴$a = -1$。
故抛物线的函数解析式为$y = -x^2 - 2x + 3$。
(2)设直线$AB$的函数解析式为$y = kx + b$。
∵$A(-3, 0)$,$B(0, 3)$,
∴$\begin{cases}-3k + b = 0\\b = 3\end{cases}$,解得$\begin{cases}k = 1\\b = 3\end{cases}$。
故直线$AB$的函数解析式为$y = x + 3$。
如图,过点$P$作$PQ\perp x$轴于点$Q$,交直线$AB$于点$M$。

设$P(x, -x^2 - 2x + 3)$,则$M(x, x + 3)$。
∴$PM = -x^2 - 2x + 3 - (x + 3)= -x^2 - 3x$。
∴$S_{\triangle PAB} = \frac{1}{2}(-x^2 - 3x)×3 = -\frac{3}{2}(x + \frac{3}{2})^2 + \frac{27}{8}$。
∵$-\frac{3}{2} < 0$,
∴当$x = -\frac{3}{2}$时,$S_{\triangle PAB}$有最大值,$S_{最大}=\frac{27}{8}$。
此时$y = -(-\frac{3}{2})^2 - 2×(-\frac{3}{2}) + 3 = \frac{15}{4}$,
∴$\triangle PAB$的面积的最大值为$\frac{27}{8}$,此时点$P$的坐标为$(-\frac{3}{2}, \frac{15}{4})$。
(1)
∵抛物线的对称轴是直线$x = -1$且经过点$A(-3, 0)$,
∴由抛物线的对称性可知抛物线还经过点$(1, 0)$。
设抛物线的函数解析式为$y = a(x - 1)(x + 3)$。
把$B(0, 3)$代入,得$3 = -3a$,
∴$a = -1$。
故抛物线的函数解析式为$y = -x^2 - 2x + 3$。
(2)设直线$AB$的函数解析式为$y = kx + b$。
∵$A(-3, 0)$,$B(0, 3)$,
∴$\begin{cases}-3k + b = 0\\b = 3\end{cases}$,解得$\begin{cases}k = 1\\b = 3\end{cases}$。
故直线$AB$的函数解析式为$y = x + 3$。
如图,过点$P$作$PQ\perp x$轴于点$Q$,交直线$AB$于点$M$。

设$P(x, -x^2 - 2x + 3)$,则$M(x, x + 3)$。
∴$PM = -x^2 - 2x + 3 - (x + 3)= -x^2 - 3x$。
∴$S_{\triangle PAB} = \frac{1}{2}(-x^2 - 3x)×3 = -\frac{3}{2}(x + \frac{3}{2})^2 + \frac{27}{8}$。
∵$-\frac{3}{2} < 0$,
∴当$x = -\frac{3}{2}$时,$S_{\triangle PAB}$有最大值,$S_{最大}=\frac{27}{8}$。
此时$y = -(-\frac{3}{2})^2 - 2×(-\frac{3}{2}) + 3 = \frac{15}{4}$,
∴$\triangle PAB$的面积的最大值为$\frac{27}{8}$,此时点$P$的坐标为$(-\frac{3}{2}, \frac{15}{4})$。
查看更多完整答案,请扫码查看


