《2025年初中同步练习册分层卷九年级数学上册人教版》

6. (4分)点$A(m - 1, y_1)$,$B(m, y_2)都在二次函数y = (x - 1)^2 + n$的图象上.若$y_1 ＜ y_2$,则$m$的取值范围为( )
[A] $m ＞ 2$

[B] $m ＞ \frac{3}{2}$
[C] $m ＜ 1$
[D] $\frac{3}{2} ＜ m ＜ 2$

答案： B

7. (10分)已知函数$y = -x^2 + bx + c$($b$,$c$为常数)的图象经过点$(0, -3)$,$(-6, -3)$.
(1)求$b$,$c$的值；
(2)当$-4 \leq x \leq 0$时,求$y$的最大值；
(3)当$m \leq x \leq 0$时,若$y的最大值与最小值之和为2$,求$m$的值.

答案： 解：（1）把（0，-3），（-6，-3）代入$y=-x^{2}+bx+c$，得$b=-6$，$c=-3$.
（2）$\because y=-x^{2}-6x-3=-(x+3)^{2}+6$，$-4\leqslant x\leqslant0$，$\therefore$当$x=-3$时，$y$有最大值，最大值为6.
（3）①当$-3＜m\leqslant0$时，当$x=0$时，$y$有最小值，为-3.当$x=m$时，$y$有最大值，为$-m^{2}-6m-3$.$\because y$的最大值与最小值之和为2，$\therefore -m^{2}-6m-3+(-3)=2$.$\therefore m_{1}=-2$，$m_{2}=-4$(舍去).②当$m\leqslant-3$时，当$x=-3$时，$y$有最大值，为6.$\because y$的最大值与最小值之和为2，$\therefore y$的最小值为-4.$\therefore -(m+3)^{2}+6=-4$.$\therefore m_{1}=-3-\sqrt{10}$，$m_{2}=-3+\sqrt{10}$(舍去).综上所述，$m=-2$或$m=-3-\sqrt{10}$.

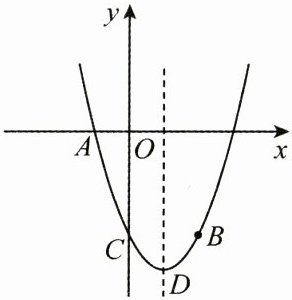
8. (10分)如图,抛物线$y = x^2 + bx + c经过点A(-1, 0)$,$B(2, -3)$,与$y轴交于点C$,抛物线的顶点为$D$.
(1)求抛物线的函数解析式.
(2)抛物线上是否存在点$P$,使$\triangle PBC的面积是\triangle BCD面积的4$倍？若存在,请求出点$P$的坐标；若不存在,请说明理由.

答案： 解：（1）$\because$抛物线$y=x^{2}+bx+c$经过点$A(-1,0)$，$B(2,-3)$，$\therefore \begin{cases} 1-b+c=0, \\ 4+2b+c=-3, \end{cases}$解得$\begin{cases} b=-2, \\ c=-3. \end{cases}$$\therefore$抛物线的函数解析式为$y=x^{2}-2x-3$.
（2）存在.$\because y=x^{2}-2x-3=(x-1)^{2}-4$，$\therefore$点$D$的坐标为$(1,-4)$.令$x=0$，则$y=x^{2}-2x-3=-3$，$\therefore$点$C$的坐标为$(0,-3)$.又$\because$点$B$的坐标为$(2,-3)$，$\therefore BC// x$轴.$\therefore S_{\triangle BCD}=\frac{1}{2}×2×1=1$.设抛物线上的点$P$的坐标为$(m,m^{2}-2m-3)$，$\therefore S_{\triangle PBC}=\frac{1}{2}×2×|m^{2}-2m-3-(-3)|=|m^{2}-2m|$.当$|m^{2}-2m|=4×1$时，解得$m=1\pm\sqrt{5}$.当$m=1+\sqrt{5}$时，$m^{2}-2m-3=1$；当$m=1-\sqrt{5}$时，$m^{2}-2m-3=1$.综上所述，点$P$的坐标为$(1+\sqrt{5},1)$或$(1-\sqrt{5},1)$.