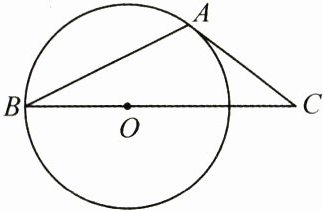
14. (4分)如图,在△ABC中,AC= 2,BC= 4,点O在BC上,以点O为圆心、OB长为半径的圆与AC相切于点A.D是边BC上的动点,当△ACD为直角三角形时,AD的长为______.

答案:
$\frac{3}{2}$或$\frac{6}{5}$
15. (12分)已知AB为⊙O的直径,C为⊙O上一点,D为BA延长线上的一点,连接CD.
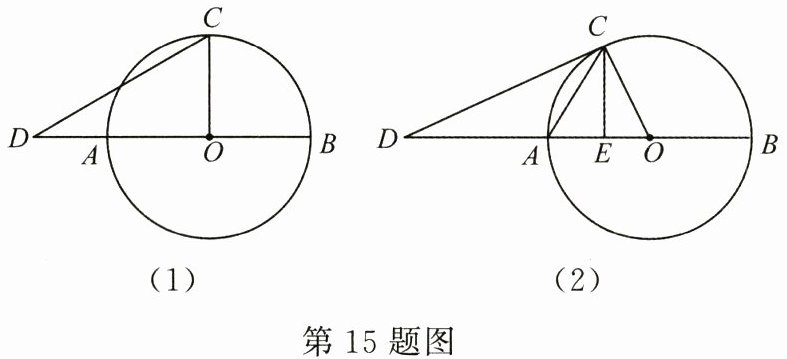
(1)如图(1),若CO⊥AB,∠D= 30°,OA= 1,求AD的长;
(2)如图(2),若DC与⊙O相切,E为OA上一点,且∠ACD= ∠ACE.求证:CE⊥AB.
(1)如图(1),若CO⊥AB,∠D= 30°,OA= 1,求AD的长;
(2)如图(2),若DC与⊙O相切,E为OA上一点,且∠ACD= ∠ACE.求证:CE⊥AB.

答案:
(1)解:
∵OC=OA=1,CO⊥AB,∠D=30°,
∴CD=2,OD=$\sqrt{3}$.
∴AD=OD - OA=$\sqrt{3}-1$.
(2)证明:
∵DC与$\odot O$相切,
∴OC⊥DC,即∠ACD+∠OCA=90°.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠ACD=∠ACE,
∴∠OAC+∠ACE=90°.
∴∠AEC=90°,即CE⊥AB.
(1)解:
∵OC=OA=1,CO⊥AB,∠D=30°,
∴CD=2,OD=$\sqrt{3}$.
∴AD=OD - OA=$\sqrt{3}-1$.
(2)证明:
∵DC与$\odot O$相切,
∴OC⊥DC,即∠ACD+∠OCA=90°.
∵OA=OC,
∴∠OCA=∠OAC.
∵∠ACD=∠ACE,
∴∠OAC+∠ACE=90°.
∴∠AEC=90°,即CE⊥AB.
查看更多完整答案,请扫码查看


