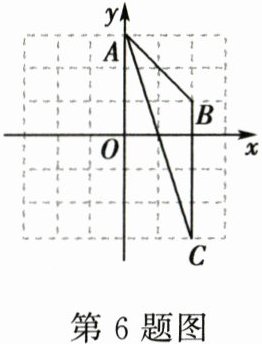
6. 如图,在平面直角坐标系中,点 $ A $ 的坐标为 $ (0,3) $,点 $ B $ 的坐标为 $ (2,1) $,点 $ C $ 的坐标为 $ (2,-3) $.经画图操作,可知 $ \triangle ABC $ 的外心的坐标是( )
[A] $ (-2,-1) $ [B] $ (1,0) $ [C] $ (0,0) $ [D] $ (2,0) $
[A] $ (-2,-1) $ [B] $ (1,0) $ [C] $ (0,0) $ [D] $ (2,0) $

答案:
A
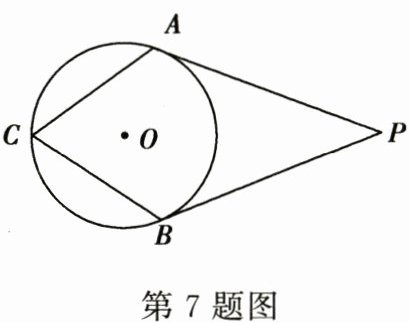
7. 如图,$ PA $,$ PB $ 分别切 $ \odot O $ 于 $ A $,$ B $ 两点.若 $ \angle P = 40^{\circ} $,则 $ \angle C $ 的度数为( )
[A] $ 40^{\circ} $ [B] $ 140^{\circ} $ [C] $ 70^{\circ} $ [D] $ 80^{\circ} $
[A] $ 40^{\circ} $ [B] $ 140^{\circ} $ [C] $ 70^{\circ} $ [D] $ 80^{\circ} $

答案:
C
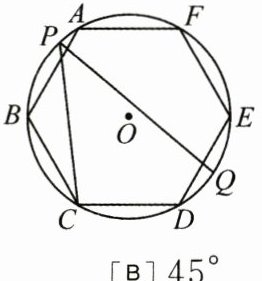
8. 如图,正六边形 $ ABCDEF $ 内接于 $ \odot O $,点 $ P $ 在 $ \overset{\frown}{AB} $ 上,$ Q $ 是 $ \overset{\frown}{DE} $ 的中点,则 $ \angle CPQ $ 的度数为( )
[A] $ 30^{\circ} $ [B] $ 45^{\circ} $ [C] $ 36^{\circ} $ [D] $ 60^{\circ} $
[A] $ 30^{\circ} $ [B] $ 45^{\circ} $ [C] $ 36^{\circ} $ [D] $ 60^{\circ} $

答案:
B
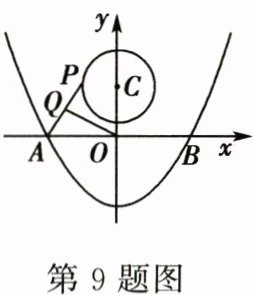
9. 如图,抛物线 $ y = \frac{1}{4}x^{2} - 4 $ 与 $ x $ 轴交于 $ A $,$ B $ 两点,$ P $ 是以点 $ C(0,3) $ 为圆心、$ 2 $ 为半径的圆上的动点,$ Q $ 是线段 $ PA $ 的中点,连接 $ OQ $,则线段 $ OQ $ 的最大值是( )
[A] $ 3 $ [B] $ \frac{\sqrt{41}}{2} $ [C] $ \frac{7}{2} $ [D] $ 4 $
[A] $ 3 $ [B] $ \frac{\sqrt{41}}{2} $ [C] $ \frac{7}{2} $ [D] $ 4 $

答案:
C
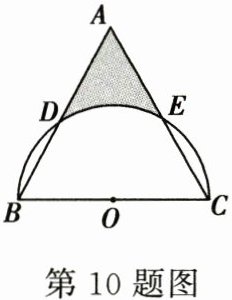
10. 如图,等边三角形 $ ABC $ 的边长为 $ 4 $,以 $ BC $ 为直径的半圆 $ O $ 交 $ AB $ 于点 $ D $,交 $ AC $ 于点 $ E $,则图中阴影部分的面积是( )
[A] $ 2\sqrt{3} - \frac{\pi}{3} $ [B] $ 2\sqrt{3} - \frac{2\pi}{3} $ [C] $ 4\sqrt{3} - \frac{\pi}{3} $ [D] $ 4\sqrt{3} - \frac{2\pi}{3} $
[A] $ 2\sqrt{3} - \frac{\pi}{3} $ [B] $ 2\sqrt{3} - \frac{2\pi}{3} $ [C] $ 4\sqrt{3} - \frac{\pi}{3} $ [D] $ 4\sqrt{3} - \frac{2\pi}{3} $

答案:
B
查看更多完整答案,请扫码查看


