第58页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
一作图确定位置
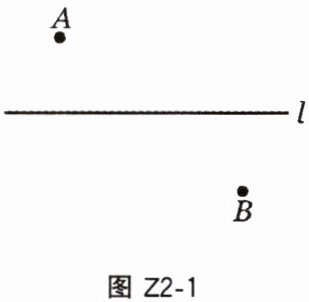
1. 如图 Z2 - 1,点 A,B 分别是直线 l 异侧的两个点,如何在 l 上找一个点 C,使得点 C 到点 A,B 的距离之和最小?
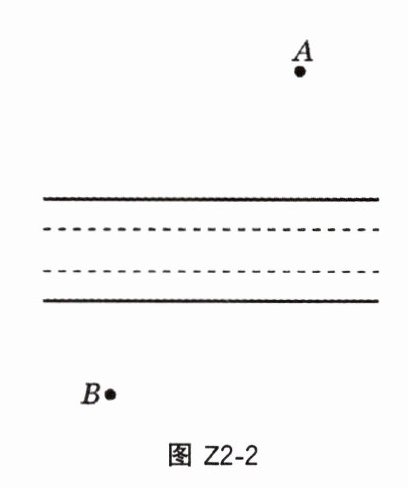
2. 如图 Z2 - 2,从 A 地到 B 地经过一条小河(河岸平行),欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从 A 地到 B 地的路程最短?
3. 如图 Z2 - 3,小河边有两个村庄 A,B,要在河边 EF 建一个自来水厂向 A 村与 B 村供水.
(1)若要使厂部到 A,B 村的距离相等,则应选择在哪里建厂?请画图说明.
(2)若要使厂部到 A,B 两村的水管最短,应建在什么地方?请画图说明.

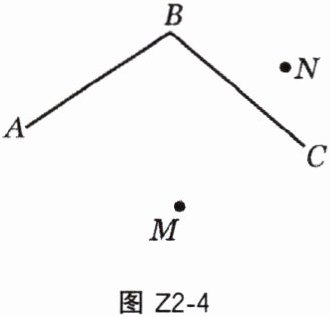
4. 如图 Z2 - 4,已知∠ABC 及点 M,N,求作点 P,使得 PM = PN,且点 P 到∠ABC 的两边的距离相等.
1. 如图 Z2 - 1,点 A,B 分别是直线 l 异侧的两个点,如何在 l 上找一个点 C,使得点 C 到点 A,B 的距离之和最小?

2. 如图 Z2 - 2,从 A 地到 B 地经过一条小河(河岸平行),欲在河上建一座与两岸垂直的桥,应如何选择桥的位置才能使从 A 地到 B 地的路程最短?

3. 如图 Z2 - 3,小河边有两个村庄 A,B,要在河边 EF 建一个自来水厂向 A 村与 B 村供水.
(1)若要使厂部到 A,B 村的距离相等,则应选择在哪里建厂?请画图说明.
(2)若要使厂部到 A,B 两村的水管最短,应建在什么地方?请画图说明.

4. 如图 Z2 - 4,已知∠ABC 及点 M,N,求作点 P,使得 PM = PN,且点 P 到∠ABC 的两边的距离相等.

答案:
1. 连接AB,AB与直线l的交点即为点C。
2. 过点A作河岸的垂线,在垂线上截取AA'等于河宽,连接A'B,与靠近B地的河岸交于点C,过点C作河岸的垂线交另一河岸于点D,CD即为桥的位置。
3.
(1)作线段AB的垂直平分线,与EF的交点即为建厂位置。
(2)作点A关于EF的对称点A',连接A'B,与EF的交点即为建厂位置。
4. 作∠ABC的角平分线和线段MN的垂直平分线,两条线的交点即为点P。
2. 过点A作河岸的垂线,在垂线上截取AA'等于河宽,连接A'B,与靠近B地的河岸交于点C,过点C作河岸的垂线交另一河岸于点D,CD即为桥的位置。
3.
(1)作线段AB的垂直平分线,与EF的交点即为建厂位置。
(2)作点A关于EF的对称点A',连接A'B,与EF的交点即为建厂位置。
4. 作∠ABC的角平分线和线段MN的垂直平分线,两条线的交点即为点P。
二求作等腰三角形
5. 已知等腰三角形,请分别画图解答下列各题:
(1)若一腰的垂直平分线与另一腰的夹角是 50°,则作图①,得顶角的度数为
(2)若一腰的垂直平分线与另一腰的延长线的夹角为 50°,则作图②,得顶角的度数为
(3)若一腰的垂直平分线与另一腰所在直线的夹角为 50°,则作图③,得顶角的度数为
悟:交点位置与等腰三角形的形状有关,应注意运用分类讨论思想.
5. 已知等腰三角形,请分别画图解答下列各题:
(1)若一腰的垂直平分线与另一腰的夹角是 50°,则作图①,得顶角的度数为
40°
;(2)若一腰的垂直平分线与另一腰的延长线的夹角为 50°,则作图②,得顶角的度数为
140°
;(3)若一腰的垂直平分线与另一腰所在直线的夹角为 50°,则作图③,得顶角的度数为
40°或140°
.悟:交点位置与等腰三角形的形状有关,应注意运用分类讨论思想.
答案:
5.(1)40° (2)140° (3),40°或140°
6. 若等腰三角形一腰上的高与另一腰的夹角为 40°,则这个等腰三角形的顶角的度数为____.
答案:
50°或130°
7. 如图 Z2 - 5,在△ABC 中,AB = AC,∠A = 36°,请设计一种分法,将△ABC 分割成三个等腰三角形,并标出每个等腰三角形的内角度数.

答案:
1. 首先求$\angle B$和$\angle C$的度数:
因为$AB = AC$,根据三角形内角和定理$\angle A+\angle B+\angle C = 180^{\circ}$,且$\angle B=\angle C$,已知$\angle A = 36^{\circ}$,则$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}$。
把$\angle A = 36^{\circ}$代入$\angle B=\angle C=\frac{180 - 36}{2}$,可得$\angle B=\angle C = 72^{\circ}$。
2. 然后进行分割:
作$\angle B$的平分线$BD$交$AC$于$D$,再作$DE// AB$交$BC$于$E$。
对于$\triangle ABD$:
因为$\angle A = 36^{\circ}$,$\angle ABD=\frac{1}{2}\angle B$,$\angle B = 72^{\circ}$,所以$\angle ABD = 36^{\circ}$,则$\angle ADB=180^{\circ}-\angle A-\angle ABD=180 - 36-36 = 108^{\circ}$,所以$\triangle ABD$是等腰三角形($\angle A=\angle ABD = 36^{\circ}$,$AD = BD$)。
对于$\triangle BDE$:
因为$DE// AB$,所以$\angle EDB=\angle ABD = 36^{\circ}$,$\angle BED = 180^{\circ}-\angle EDB-\angle EBD$,$\angle EBD=\frac{1}{2}\angle B = 36^{\circ}$,则$\angle BED = 108^{\circ}$,$\angle BDE=\angle DBE = 36^{\circ}$,所以$\triangle BDE$是等腰三角形($BE = DE$)。
对于$\triangle DEC$:
因为$DE// AB$,$AB = AC$,所以$\angle DEC=\angle B = 72^{\circ}$,$\angle C = 72^{\circ}$,则$\angle EDC=180^{\circ}-\angle DEC-\angle C=180 - 72-72 = 36^{\circ}$,所以$\triangle DEC$是等腰三角形($\angle DEC=\angle C = 72^{\circ}$,$DE = DC$)。
或者:
作$\angle B$的平分线$BD$交$AC$于$D$,再作$\angle BDC$的平分线$DE$交$BC$于$E$。
对于$\triangle ABD$:
因为$\angle A = 36^{\circ}$,$\angle ABD=\frac{1}{2}\angle B$,$\angle B = 72^{\circ}$,所以$\angle ABD = 36^{\circ}$,$\angle ADB = 108^{\circ}$,$\triangle ABD$是等腰三角形($\angle A=\angle ABD = 36^{\circ}$,$AD = BD$)。
对于$\triangle BDE$:
因为$\angle BDC = 180^{\circ}-\angle ADB=72^{\circ}$,$\angle BDE=\frac{1}{2}\angle BDC = 36^{\circ}$,$\angle DBE = 36^{\circ}$,所以$\angle BED = 108^{\circ}$,$\triangle BDE$是等腰三角形($\angle BDE=\angle DBE = 36^{\circ}$,$BE = DE$)。
对于$\triangle DEC$:
因为$\angle EDC=\frac{1}{2}\angle BDC = 36^{\circ}$,$\angle C = 72^{\circ}$,所以$\angle DEC = 72^{\circ}$,$\triangle DEC$是等腰三角形($\angle DEC=\angle C = 72^{\circ}$,$DE = DC$)。
具体角度标注:
等腰$\triangle ABD$:$\angle A = 36^{\circ}$,$\angle ABD = 36^{\circ}$,$\angle ADB = 108^{\circ}$;
等腰$\triangle BDE$:$\angle BDE = 36^{\circ}$,$\angle DBE = 36^{\circ}$,$\angle BED = 108^{\circ}$;
等腰$\triangle DEC$:$\angle DEC = 72^{\circ}$,$\angle EDC = 36^{\circ}$,$\angle C = 72^{\circ}$。(分法不唯一)
因为$AB = AC$,根据三角形内角和定理$\angle A+\angle B+\angle C = 180^{\circ}$,且$\angle B=\angle C$,已知$\angle A = 36^{\circ}$,则$\angle B=\angle C=\frac{180^{\circ}-\angle A}{2}$。
把$\angle A = 36^{\circ}$代入$\angle B=\angle C=\frac{180 - 36}{2}$,可得$\angle B=\angle C = 72^{\circ}$。
2. 然后进行分割:
作$\angle B$的平分线$BD$交$AC$于$D$,再作$DE// AB$交$BC$于$E$。
对于$\triangle ABD$:
因为$\angle A = 36^{\circ}$,$\angle ABD=\frac{1}{2}\angle B$,$\angle B = 72^{\circ}$,所以$\angle ABD = 36^{\circ}$,则$\angle ADB=180^{\circ}-\angle A-\angle ABD=180 - 36-36 = 108^{\circ}$,所以$\triangle ABD$是等腰三角形($\angle A=\angle ABD = 36^{\circ}$,$AD = BD$)。
对于$\triangle BDE$:
因为$DE// AB$,所以$\angle EDB=\angle ABD = 36^{\circ}$,$\angle BED = 180^{\circ}-\angle EDB-\angle EBD$,$\angle EBD=\frac{1}{2}\angle B = 36^{\circ}$,则$\angle BED = 108^{\circ}$,$\angle BDE=\angle DBE = 36^{\circ}$,所以$\triangle BDE$是等腰三角形($BE = DE$)。
对于$\triangle DEC$:
因为$DE// AB$,$AB = AC$,所以$\angle DEC=\angle B = 72^{\circ}$,$\angle C = 72^{\circ}$,则$\angle EDC=180^{\circ}-\angle DEC-\angle C=180 - 72-72 = 36^{\circ}$,所以$\triangle DEC$是等腰三角形($\angle DEC=\angle C = 72^{\circ}$,$DE = DC$)。
或者:
作$\angle B$的平分线$BD$交$AC$于$D$,再作$\angle BDC$的平分线$DE$交$BC$于$E$。
对于$\triangle ABD$:
因为$\angle A = 36^{\circ}$,$\angle ABD=\frac{1}{2}\angle B$,$\angle B = 72^{\circ}$,所以$\angle ABD = 36^{\circ}$,$\angle ADB = 108^{\circ}$,$\triangle ABD$是等腰三角形($\angle A=\angle ABD = 36^{\circ}$,$AD = BD$)。
对于$\triangle BDE$:
因为$\angle BDC = 180^{\circ}-\angle ADB=72^{\circ}$,$\angle BDE=\frac{1}{2}\angle BDC = 36^{\circ}$,$\angle DBE = 36^{\circ}$,所以$\angle BED = 108^{\circ}$,$\triangle BDE$是等腰三角形($\angle BDE=\angle DBE = 36^{\circ}$,$BE = DE$)。
对于$\triangle DEC$:
因为$\angle EDC=\frac{1}{2}\angle BDC = 36^{\circ}$,$\angle C = 72^{\circ}$,所以$\angle DEC = 72^{\circ}$,$\triangle DEC$是等腰三角形($\angle DEC=\angle C = 72^{\circ}$,$DE = DC$)。
具体角度标注:
等腰$\triangle ABD$:$\angle A = 36^{\circ}$,$\angle ABD = 36^{\circ}$,$\angle ADB = 108^{\circ}$;
等腰$\triangle BDE$:$\angle BDE = 36^{\circ}$,$\angle DBE = 36^{\circ}$,$\angle BED = 108^{\circ}$;
等腰$\triangle DEC$:$\angle DEC = 72^{\circ}$,$\angle EDC = 36^{\circ}$,$\angle C = 72^{\circ}$。(分法不唯一)
查看更多完整答案,请扫码查看


