《2025年顶尖课课练八年级数学上册人教版》

2. 如图 13.3.2 - 2,在△ABC 中,∠A = 50°,∠ABC = 70°,BD 平分∠ABC,则∠BDC 的度数为(A).

A.85°
B.80°
C.75°
D.70°

答案： A

3. 如图 13.3.2 - 3,根据图中的条件,直接写出∠1 的度数：

(1)图①中,∠1 = 85°；
(2)图②中,∠1 = 100°；
(3)图③中,∠1 = 85°.

答案： （1）85° （2）100° （3）85°

4. 将一副三角尺按如图 13.3.2 - 4 所示的方式摆放,则∠α 的度数为75°.

答案： 75°

5. 将一副三角尺按如图 13.3.2 - 5 所示的方式摆放,点 C,B,E 共线,∠FEB = 63°,则∠EDB 的度数为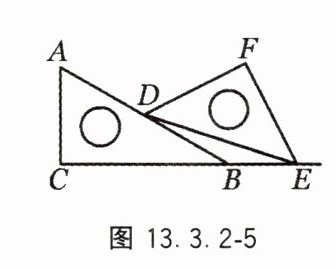12°.

答案： 12°

6. 如图 13.3.2 - 6,AB // CD,∠D = 65°,∠B = 36°,求∠E 的度数.

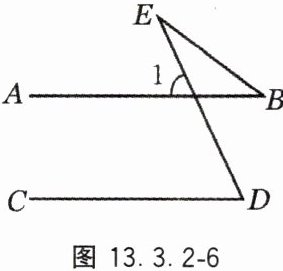
答案： 29°

7. 图 13.3.2 - 7 是可调躺椅示意图(数据如图),AE 与 BD 的交点为 C,且∠A,∠B,∠E 保持不变,为了舒适,需调整∠D 的大小,使∠EFD = 110°,则图中∠D 应(B).

A.增加 10°
B.减少 10°
C.增加 20°
D.减少 20°

答案： B

8. 某零件的示意图如图 13.3.2 - 8 所示,图纸要求∠A = 90°,∠B = 32°,∠C = 21°. 当检验员量得∠BDC = 145°时,就断定这个零件不合格,你能说出其中的道理吗？

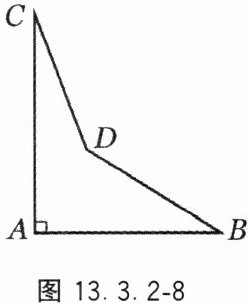
答案： 延长AD至点E。
∵∠CDE是△ACD的外角，
∴∠CDE=∠C+∠CAD。
∵∠BDE是△ABD的外角，
∴∠BDE=∠B+∠BAD。
∵∠BDC=∠CDE+∠BDE，
∴∠BDC=∠C+∠CAD+∠B+∠BAD=∠B+∠C+∠BAC。
∵∠BAC=90°，∠B=32°，∠C=21°，
∴∠BDC=32°+21°+90°=143°。
∵检验员量得∠BDC=145°≠143°，
∴该零件不合格。

2. 小明计算出一个多边形的内角和是 2750°,同桌小华发现小明漏加了一个角.
(1)求小明漏加的那个角的度数；
(2)问：小明求的是几边形的内角和？
三 用方程思想求三角形的角

答案：
(1) 设漏加的那个角的度数为 $x^{\circ}$，多边形的边数为 $n$。
根据多边形内角和公式，有：
$2750^{\circ} + x^{\circ} = (n - 2) × 180^{\circ}$，
由于 $x$ 是多边形的一个内角，所以 $0^{\circ} ＜ x ＜ 180^{\circ}$。
将 $2750^{\circ}$ 除以 $180^{\circ}$ 得到：
$2750 ÷ 180 = 15\ldots 50$，
即 $2750^{\circ} = 15 × 180^{\circ} + 50^{\circ}$。
由此可得：
$x = 180 - 50 = 130^{\circ}$。
(2) 将 $x = 130^{\circ}$ 代入 $2750^{\circ} + x^{\circ} = (n - 2) × 180^{\circ}$，得：
$2750 + 130 = (n - 2) × 180$，
$2880 = (n - 2) × 180$，
$n - 2 = 16$，
$n = 18$。
故（1）小明漏加的那个角的度数为 $130^{\circ}$；（2）小明求的是十八边形的内角和。