《2025年顶尖课课练八年级数学上册人教版》

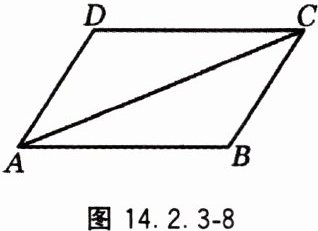
9. 如图14.2.3-8,在四边形ABCD中,AD= BC,AB= CD,求证：
(1)△ABC≌△CDA；
(2)DC//AB。

答案：
(1)
在$\triangle ABC$和$\triangle CDA$中，
$AB = CD$，$AD = BC$，$AC = CA$（公共边），
根据全等三角形判定定理（SSS），$\triangle ABC\cong\triangle CDA$。
(2)
由
(1)知$\triangle ABC\cong\triangle CDA$，
所以$\angle BAC=\angle DCA$，
因为内错角相等，两直线平行，
所以$DC// AB$。

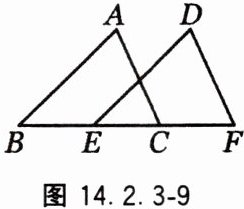
10. 如图14.2.3-9,点B,E,C,F在同一条直线上,AB= DE,AC= DF,BE= CF,求证：
(1)∠A= ∠D；
(2)AB//DE。

答案：
(1) 证明：
由于 $BE = CF$，
则 $BE + EC = CF + EC$，
即 $BC = EF$。
在 $\triangle ABC$ 与 $\triangle DEF$ 中，
$AB = DE$，$AC = DF$，$BC = EF$，
根据 SSS 全等条件，$\triangle ABC \cong \triangle DEF$，
所以 $\angle A = \angle D$。
(2) 证明：
由于 $\triangle ABC \cong \triangle DEF$，
则 $\angle B = \angle DEF$。
因为同位角相等，两直线平行，
所以 $AB // DE$。

11. (数学活动)去公园的路上,淘淘发现路边的一根电线杆两侧对称地拉着钢绳(如图14.2.3-10①),他很快明白了其中的道理。
【提出问题】淘淘来到公园,看到公园的彩旗杆两侧并没有拉着钢绳,于是提出问题：公园的彩旗杆是否垂直于地面？
【实践操作】如图14.2.3-10②,淘淘找来两根5m长的绳子,一端系在旗杆上的同一位置A处,另一端分别固定在地面的两个木桩B,C上(两个木桩和彩旗杆在同一平面内,绳结处的长度误差忽略不计),淘淘现只有一把卷尺。
【解决问题】(1)如图14.2.3-10①,电线杆两侧对称地拉着钢绳是为了防止电线杆倾倒,这样做是利用了三角形的稳定性；
(2)如图14.2.3-10②,需要用卷尺测量哪些线段的长度？
线段 BD，CD 的长度
(3)如图14.2.3-10②,当测量出的线段满足什么条件时,彩旗杆是垂直于地面的？请说明理由。
BD=CD，理由略

答案： （1）三角形的稳定性 （2）线段 BD，CD 的长度 （3）BD=CD，理由略

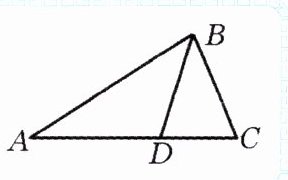
灵机一动 3. 如图,在△ABC中,AB＞BC,∠ABC的平分线交AC于点D,求证：AD＞DC。

答案： 证明：过点D作DM⊥AB于M，DN⊥BC于N。
∵BD平分∠ABC，
∴DM=DN（角的平分线上的点到角的两边的距离相等）。
∵S△ABD=1/2·AB·DM，S△CBD=1/2·BC·DN，且DM=DN，
∴S△ABD/S△CBD=AB/BC。
设点B到AC的距离为h，则S△ABD=1/2·AD·h，S△CBD=1/2·DC·h，
∴S△ABD/S△CBD=AD/DC。
∴AD/DC=AB/BC。
∵AB＞BC，
∴AD/DC＞1，即AD＞DC。