《2025年顶尖课课练八年级数学上册人教版》

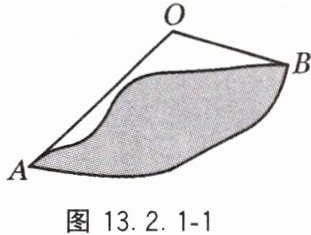
7. 如图 13.2.1 - 1,为估计池塘岸边 $ A $,$ B $ 的距离,小杰在池塘的一侧选取一点 $ O $,测得 $ OA = 10 $ m,$ OB = 6 $ m,则 $ A $,$ B $ 间的距离可能是(B).

A.4 m
B.12 m
C.16 m
D.22 m
]

答案： B

8. 现有四根长分别为 12 cm,10 cm,8 cm,4 cm 的木棒,选其中三根组成三角形,有几种选法？为什么？

答案： 从四根木棒中选三根，共有4种组合方式，分别记为：
$12 cm, 10 cm, 8 cm$：
$10+8=18 ＞ 12$，$10+12=22 ＞ 8$，$8+12=20 ＞ 10$。
满足三角形的两边之和大于第三边，所以能构成三角形。
$12 cm, 10 cm, 4 cm$：
$10+4=14 ＞ 12$，$10+12=22 ＞ 4$，$4+12=16 ＞ 10$。
满足三角形的两边之和大于第三边，所以能构成三角形。
$12 cm, 8 cm, 4 cm$：
$8+4=12$，不满足三角形的两边之和大于第三边，所以不能构成三角形。
$10 cm, 8 cm, 4 cm$：
$10+8=18 ＞ 4$，$10+4=14 ＞ 8$，$8+4=12 ＞ 10$。
满足三角形的两边之和大于第三边，所以能构成三角形。
综上，有3种选法，分别为：$12 cm, 10 cm, 8 cm$；$12 cm, 10 cm, 4 cm$；$10 cm, 8 cm, 4 cm$。

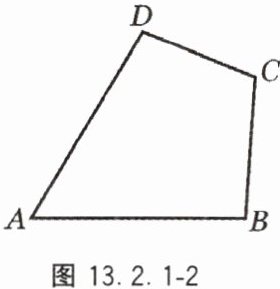
9. 如图 13.2.1 - 2,草原上有 4 口油井,分别位于四边形 $ ABCD $ 的 4 个顶点,现在要建立一个维修站 $ H $,试问：维修站 $ H $ 应建在何处,才能使它到 4 口油井的距离之和 $ AH + HB + HC + HD $ 最小？

答案： 连接四边形$ABCD$的对角线$AC$和$BD$，它们的交点即为维修站$H$的位置。
理由：根据两点之间线段最短及三角形三边关系，对于任意点$H$，有$AH + HC \geq AC$（当且仅当$H$在$AC$上时取等号），$BH + HD \geq BD$（当且仅当$H$在$BD$上时取等号）。故当$H$为$AC$与$BD$的交点时，$AH + HB + HC + HD = AC + BD$，此时距离之和最小。
结论：维修站$H$应建在对角线$AC$与$BD$的交点处。

10. 已知 $ a $,$ b $,$ c $ 是 $ \triangle ABC $ 的三边长,化简：$ |a + b - c| - |b - a - c| $.

答案： 2b-2c

11. 我国建造的港珠澳大桥全长约 55 km,是世界最长的跨海大桥. 如图 13.2.1 - 3 所示的是港珠澳大桥中的斜拉索桥,那么你能推断出斜拉索大桥中运用的数学原理是(B).

A.三角形的不稳定性
B.三角形的稳定性
C.四边形的不稳定性
D.四边形的稳定性

答案： B

12. 如图 13.2.1 - 4,王师傅用 4 根木条钉成一个四边形木架,若要使这个木架不变形,则他至少要再钉上的木条的根数是(B).

A.0
B.1
C.2
D.3
我这样想 1. 提示：利用面积法,连接 $ PA $,$ PB $,$ PC $,则 $ S_{\triangle PAB} + S_{\triangle PBC} + S_{\triangle PAC} = S_{\triangle ABC} $.

答案： B