第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
2. 如图 14.3.1 - 2,在 Rt△ABC 中,BD 平分∠ABC,DE⊥AB 于点 E.

(1)图中相等的线段有$ \underline{
(2)与 DE 相等的线段是$ \underline{

(1)图中相等的线段有$ \underline{
DC=DE、BC=BE
} ,相等的角有 \underline{∠CBD=∠EBD、∠CDB=∠EDB、∠AED=∠ACB=∠DEB
} ;$(2)与 DE 相等的线段是$ \underline{
DC
} ,理由是 \underline{角的平分线上的点到角的两边的距离相等
}.$
答案:
(1) DC=DE、BC=BE;∠CBD=∠EBD、∠CDB=∠EDB、∠AED=∠ACB=∠DEB
(2) DC;角的平分线上的点到角的两边的距离相等
(1) DC=DE、BC=BE;∠CBD=∠EBD、∠CDB=∠EDB、∠AED=∠ACB=∠DEB
(2) DC;角的平分线上的点到角的两边的距离相等
3. 如图 14.3.1 - 3,在 Rt△ABC 中,∠C = 90°,以顶点 A 为圆心,适当长为半径画弧,分别交 AC,AB 于点 M,N,再分别以点 M,N 为圆心,大于 $\frac{1}{2}MN$ 的长为半径画弧,两弧交于点 P,作射线 AP 交边 BC 于点 D. 若 CD = 3,AB = 10,则△ABD 的面积是 \underline{
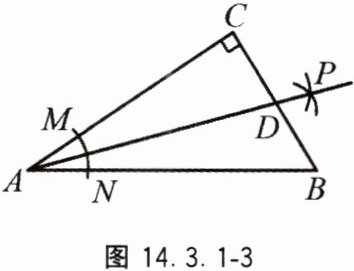
15
}.
答案:
15
4. 在△ABC 的内部取点 P,使得点 P 到△ABC 三边的距离相等,则 AP,BP,CP 均为△ABC 的(
A.高
B.角平分线
C.中线
D.以上都不是
B
).A.高
B.角平分线
C.中线
D.以上都不是
答案:
B
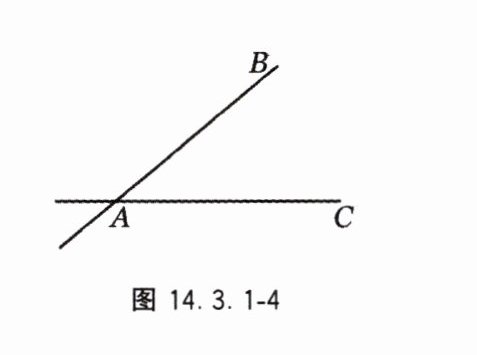
5. 如图 14.3.1 - 4,AB,AC 表示两条相交的公路,现要在∠BAC 的内部建一个物流中心. 设计时要求该物流中心到两条公路的距离相等,且到公路交叉处 A 点的距离为 1000 m.
(1)若要求以 1∶50 000 的比例尺画设计图,求物流中心到公路交叉处 A 点的图上距离;
(2)在图中画出物流中心的位置 P.
(1)若要求以 1∶50 000 的比例尺画设计图,求物流中心到公路交叉处 A 点的图上距离;
(2)在图中画出物流中心的位置 P.

答案:
(1)解:1000m=100000cm,设图上距离为$x$cm,根据比例尺$\frac{x}{100000}=\frac{1}{50000}$,解得$x = 2$。
(2)作∠BAC的角平分线,在角平分线上截取$AP = 2$cm,则点P即为所求。
(2)作∠BAC的角平分线,在角平分线上截取$AP = 2$cm,则点P即为所求。
6. 如图 14.3.1 - 5,点 O 在一块直角三角尺 ABC 上(其中∠ABC = 30°),OM⊥AB 于点 M,ON⊥BC 于点 N. 若 OM = ON,则∠ABO 的大小为$ \underline{\quad\quad}.$


答案:
$15°$
7. 如图 14.3.1 - 6,PA,PC 分别是△ABC 的外角∠MAC 和∠NCA 的平分线,它们交于点 P,PD⊥BM 于点 D,PF⊥BN 于点 F,求证:PD = PF.
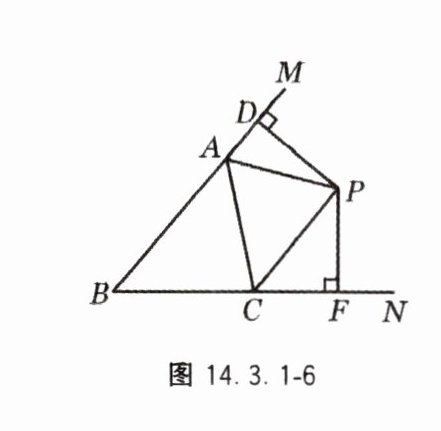

答案:
证明:过点P作PE⊥AC于点E。
∵PA平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE(角平分线上的点到角两边的距离相等)。
∵PC平分∠NCA,PF⊥CN,PE⊥AC,
∴PE=PF(角平分线上的点到角两边的距离相等)。
∴PD=PF。
∵PA平分∠MAC,PD⊥AM,PE⊥AC,
∴PD=PE(角平分线上的点到角两边的距离相等)。
∵PC平分∠NCA,PF⊥CN,PE⊥AC,
∴PE=PF(角平分线上的点到角两边的距离相等)。
∴PD=PF。
8. 如图 14.3.1 - 7,已知 BD⊥AM 于点 D,CE⊥AN 于点 E,BD,CE 交于点 F,CF = BF,求证:点 F 在∠A 的平分线上.

答案:
证明:
∵ $BD\perp AM$,$CE\perp AN$,
∴ $\angle FDC=\angle FEB=90°$。
∵ $\angle DFC=\angle EFB$(对顶角相等),$CF=BF$,
∴ $\triangle FDC\cong\triangle FEB$(AAS)。
∴ $FD=FE$。
∵ $FD\perp AM$,$FE\perp AN$,
∴ 点$F$在$\angle A$的平分线上(到角两边距离相等的点在角的平分线上)。
∵ $BD\perp AM$,$CE\perp AN$,
∴ $\angle FDC=\angle FEB=90°$。
∵ $\angle DFC=\angle EFB$(对顶角相等),$CF=BF$,
∴ $\triangle FDC\cong\triangle FEB$(AAS)。
∴ $FD=FE$。
∵ $FD\perp AM$,$FE\perp AN$,
∴ 点$F$在$\angle A$的平分线上(到角两边距离相等的点在角的平分线上)。
9. 阅读以下作图步骤:
①在 OA 和 OB 上分别截取 OC,OD,使 OC = OD;
②分别以 C,D 为圆心,以大于 $\frac{1}{2}CD$ 的长为半径作弧,两弧在∠AOB 内交于点 M;
③作射线 OM,连接 CM,DM,如图 14.3.1 - 8 所示.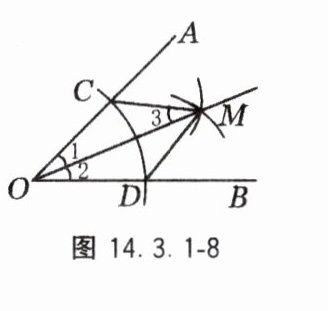
根据以上作图,一定可以推得的结论是( ).
A.∠1 = ∠2 且 CM = DM
B.∠1 = ∠3 且 CM = DM
C.∠1 = ∠2 且 OD = DM
D.∠2 = ∠3 且 OD = DM
①在 OA 和 OB 上分别截取 OC,OD,使 OC = OD;
②分别以 C,D 为圆心,以大于 $\frac{1}{2}CD$ 的长为半径作弧,两弧在∠AOB 内交于点 M;
③作射线 OM,连接 CM,DM,如图 14.3.1 - 8 所示.

根据以上作图,一定可以推得的结论是( ).
A.∠1 = ∠2 且 CM = DM
B.∠1 = ∠3 且 CM = DM
C.∠1 = ∠2 且 OD = DM
D.∠2 = ∠3 且 OD = DM
答案:
A
10. 如图 14.3.1 - 9,∠B = ∠C = 90°,点 M 是 BC 的中点,DM 平分∠ADC.

(1)求证:AM 平分∠DAB;
(2)直接写出 DC,AB 与 AD 之间的数量关系.

(1)求证:AM 平分∠DAB;
(2)直接写出 DC,AB 与 AD 之间的数量关系.
答案:
(1)证明:过点 M 作 ME⊥AD 于点 E。
∵ DM 平分∠ADC,∠C=90°,ME⊥AD,
∴ MC=ME。
∵ M 是 BC 中点,
∴ MB=MC,
∴ MB=ME。
∵ ∠B=90°,ME⊥AD,
∴ AM 平分∠DAB。
(2)DC + AB = AD
∵ DM 平分∠ADC,∠C=90°,ME⊥AD,
∴ MC=ME。
∵ M 是 BC 中点,
∴ MB=MC,
∴ MB=ME。
∵ ∠B=90°,ME⊥AD,
∴ AM 平分∠DAB。
(2)DC + AB = AD
11. 如图 14.3.1 - 10,在四边形 ABCD 中,BC>AB,AD = DC,BD 平分∠ABC,求证:∠A + ∠C = 180°.


答案:
证明:过点D作DE⊥BA交BA的延长线于E,作DF⊥BC于F。
∵BD平分∠ABC,DE⊥BA,DF⊥BC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
在Rt△ADE和Rt△CDF中,
∵AD=DC,DE=DF,
∴Rt△ADE≌Rt△CDF(HL)。
∴∠DAE=∠C(全等三角形对应角相等)。
∵∠DAE+∠BAD=180°(邻补角定义),
∴∠C+∠BAD=180°,即∠A+∠C=180°。
∵BD平分∠ABC,DE⊥BA,DF⊥BC,
∴DE=DF(角平分线上的点到角两边的距离相等)。
在Rt△ADE和Rt△CDF中,
∵AD=DC,DE=DF,
∴Rt△ADE≌Rt△CDF(HL)。
∴∠DAE=∠C(全等三角形对应角相等)。
∵∠DAE+∠BAD=180°(邻补角定义),
∴∠C+∠BAD=180°,即∠A+∠C=180°。
4. 如图,BN 平分∠ABC,点 P 为 BN 上的一点,且 PD⊥BC 于点 D,AB + BC = 2BD,求证:∠BAP + ∠BCP = 180°.

过点 $P$ 作 $PE \bot AB$,交 $AB$ 延长线于点 $E$,
因为 $BN$ 为 $\angle ABC$ 平分线,$PE \bot AB$,$PD \bot BC$,
所以 $PE = PD$,$ \angle AEP = \angle CDP = 90°$,
因为 $AB + BC = 2BD$,
$BC = BD + CD$,
$AB + BD + CD = 2BD$,
所以 $AB + CD = BD$,
$AB = BE - AE$,
$CD = CD$,
$BE - AE + CD = BD$,
因为 $BE = BD$,
所以 $CD = AE$,
在 $Rt\triangle AEP$ 和 $Rt\triangle CDP$ 中,
$\begin{cases}PE = PD,\\AE = CD.\end{cases}$
所以 $ \triangle AEP \cong \triangle CDP (SAS)$,
所以 $ \angle BAP = \angle PDC$,
因为 $ \angle PDC + \angle BCP = 180°$,
所以 $ \angle BAP + \angle BCP = 180°$。
综上,证明 $ \angle BAP + \angle BCP = 180°$。

过点 $P$ 作 $PE \bot AB$,交 $AB$ 延长线于点 $E$,
因为 $BN$ 为 $\angle ABC$ 平分线,$PE \bot AB$,$PD \bot BC$,
所以 $PE = PD$,$ \angle AEP = \angle CDP = 90°$,
因为 $AB + BC = 2BD$,
$BC = BD + CD$,
$AB + BD + CD = 2BD$,
所以 $AB + CD = BD$,
$AB = BE - AE$,
$CD = CD$,
$BE - AE + CD = BD$,
因为 $BE = BD$,
所以 $CD = AE$,
在 $Rt\triangle AEP$ 和 $Rt\triangle CDP$ 中,
$\begin{cases}PE = PD,\\AE = CD.\end{cases}$
所以 $ \triangle AEP \cong \triangle CDP (SAS)$,
所以 $ \angle BAP = \angle PDC$,
因为 $ \angle PDC + \angle BCP = 180°$,
所以 $ \angle BAP + \angle BCP = 180°$。
综上,证明 $ \angle BAP + \angle BCP = 180°$。
答案:
过点 $P$ 作 $PE \bot AB$,交 $AB$ 延长线于点 $E$,
因为 $BN$ 为 $\angle ABC$ 平分线,$PE \bot AB$,$PD \bot BC$,
所以 $PE = PD$,$ \angle AEP = \angle CDP = 90°$,
因为 $AB + BC = 2BD$,
$BC = BD + CD$,
$AB + BD + CD = 2BD$,
所以 $AB + CD = BD$,
$AB = BE - AE$,
$CD = CD$,
$BE - AE + CD = BD$,
因为 $BE = BD$,
所以 $CD = AE$,
在 $Rt\triangle AEP$ 和 $Rt\triangle CDP$ 中,
$\begin{cases}PE = PD,\\AE = CD.\end{cases}$
所以 $ \triangle AEP \cong \triangle CDP (SAS)$,
所以 $ \angle BAP = \angle PDC$,
因为 $ \angle PDC + \angle BCP = 180°$,
所以 $ \angle BAP + \angle BCP = 180°$。
综上,证明 $ \angle BAP + \angle BCP = 180°$。
因为 $BN$ 为 $\angle ABC$ 平分线,$PE \bot AB$,$PD \bot BC$,
所以 $PE = PD$,$ \angle AEP = \angle CDP = 90°$,
因为 $AB + BC = 2BD$,
$BC = BD + CD$,
$AB + BD + CD = 2BD$,
所以 $AB + CD = BD$,
$AB = BE - AE$,
$CD = CD$,
$BE - AE + CD = BD$,
因为 $BE = BD$,
所以 $CD = AE$,
在 $Rt\triangle AEP$ 和 $Rt\triangle CDP$ 中,
$\begin{cases}PE = PD,\\AE = CD.\end{cases}$
所以 $ \triangle AEP \cong \triangle CDP (SAS)$,
所以 $ \angle BAP = \angle PDC$,
因为 $ \angle PDC + \angle BCP = 180°$,
所以 $ \angle BAP + \angle BCP = 180°$。
综上,证明 $ \angle BAP + \angle BCP = 180°$。
查看更多完整答案,请扫码查看


