第44页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
7. 如图 15.2.1 - 5,以虚线为对称轴画出下列各图中已知图形的轴对称图形。
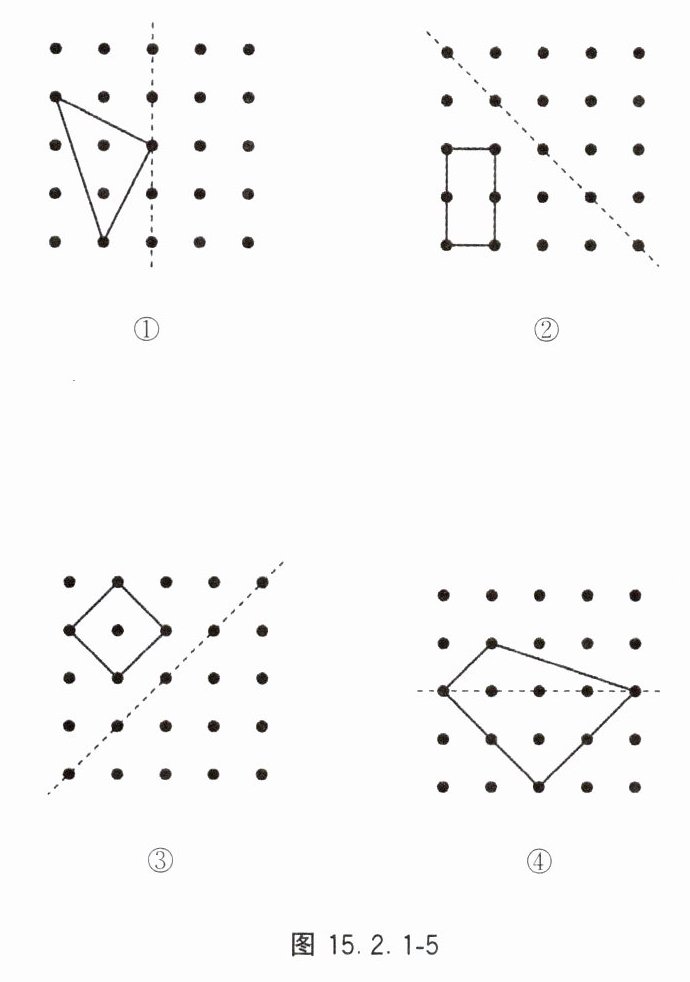

答案:
对于图1:
原图是一个三角形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图2:
原图是一个长方形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图3:
原图是一个小四边形组成的图形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图4:
原图是一个四边形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
画出的图形如下:

原图是一个三角形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图2:
原图是一个长方形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图3:
原图是一个小四边形组成的图形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
对于图4:
原图是一个四边形,以虚线为对称轴,找到每个顶点关于对称轴的对称点,依次连接,得到其轴对称图形。
画出的图形如下:

8. 如图 15.2.1 - 6,将一个正方形纸片沿对角线折叠一次,然后在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是图 15.2.1 - 7 中的(
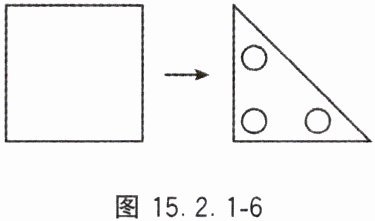
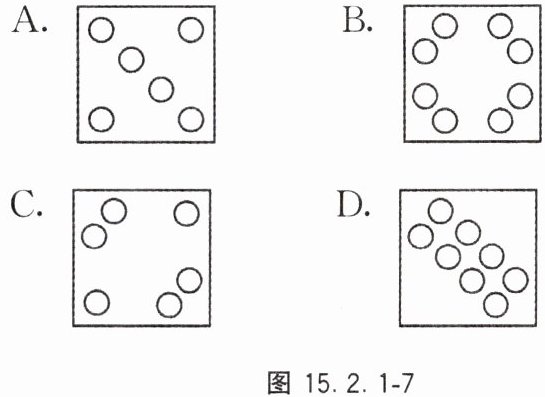
C
)。

答案:
C
9. 将圆形纸片对折后再对折,得到如图 15.2.1 - 8 所示的图形,然后沿着图中的虚线剪开,得到两部分,其中一部分展开后的平面图形是图 15.2.1 - 9 中的(
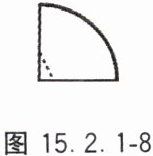
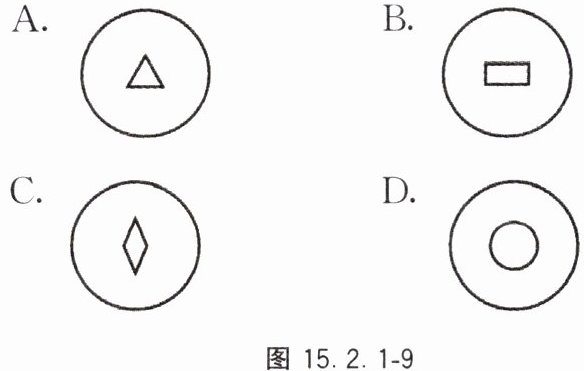
C
)。

答案:
C
10. 在平面镜里看到背后墙上的电子钟的示数如图 15.2.1 - 10 所示,这时的实际时间应该是
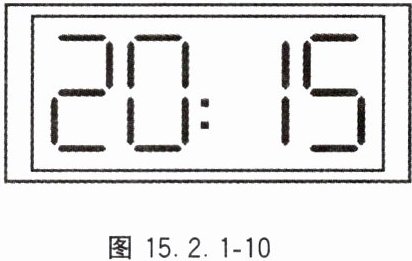
21:05
。
答案:
21:05
11. 图 15.2.1 - 11 是一个改造过的台球桌面的示意图,图中四个角上的阴影部分分别表示四个入球孔。如果一个球按图示方向被击中(球可以经过多次反射),那么该球最后将落入的球袋是(
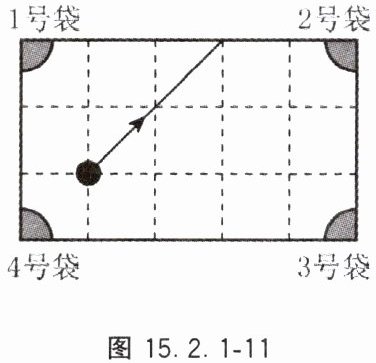
A.1 号袋
B.2 号袋
C.3 号袋
D.4 号袋
B
)。
A.1 号袋
B.2 号袋
C.3 号袋
D.4 号袋
答案:
B
12. 如图 15.2.1 - 12,已知 $ \triangle ABC $ 和直线 $ l $,$ l' $,其中 $ l // l' $,请画出 $ \triangle ABC $ 关于直线 $ l $ 的轴对称图形 $ \triangle A_1B_1C_1 $,再画出 $ \triangle A_1B_1C_1 $ 关于直线 $ l' $ 的轴对称图形 $ \triangle A_2B_2C_2 $,观察 $ \triangle ABC $ 和 $ \triangle A_2B_2C_2 $,你有什么发现?


答案:
1. 画$\triangle ABC$关于直线$l$的轴对称图形$\triangle A_1B_1C_1$:
过点$A$作$AM\perp l$,并延长使$AM = A_1M$,得点$A_1$;
过点$B$作$BN\perp l$,并延长使$BN = B_1N$,得点$B_1$;
过点$C$作$CP\perp l$,并延长使$CP = C_1P$,得点$C_1$;
顺次连接$A_1$,$B_1$,$C_1$,得到$\triangle A_1B_1C_1$。
2. 画$\triangle A_1B_1C_1$关于直线$l'$的轴对称图形$\triangle A_2B_2C_2$:
过点$A_1$作$A_1Q\perp l'$,并延长使$A_1Q = A_2Q$,得点$A_2$;
过点$B_1$作$B_1R\perp l'$,并延长使$B_1R = B_2R$,得点$B_2$;
过点$C_1$作$C_1S\perp l'$,并延长使$C_1S = C_2S$,得点$C_2$;
顺次连接$A_2$,$B_2$,$C_2$,得到$\triangle A_2B_2C_2$。
3. 观察发现:
$\triangle ABC$与$\triangle A_2B_2C_2$关于点$($两平行线$l$,$l'$中心对称(或$\triangle ABC$与$\triangle A_2B_2C_2$形状、大小相同,方向相反,且对应点所连线段平行于$l$与$l'$的间距中线或者由两次轴对称可知$\triangle ABC$与$\triangle A_2B_2C_2$成中心对称)。
过点$A$作$AM\perp l$,并延长使$AM = A_1M$,得点$A_1$;
过点$B$作$BN\perp l$,并延长使$BN = B_1N$,得点$B_1$;
过点$C$作$CP\perp l$,并延长使$CP = C_1P$,得点$C_1$;
顺次连接$A_1$,$B_1$,$C_1$,得到$\triangle A_1B_1C_1$。
2. 画$\triangle A_1B_1C_1$关于直线$l'$的轴对称图形$\triangle A_2B_2C_2$:
过点$A_1$作$A_1Q\perp l'$,并延长使$A_1Q = A_2Q$,得点$A_2$;
过点$B_1$作$B_1R\perp l'$,并延长使$B_1R = B_2R$,得点$B_2$;
过点$C_1$作$C_1S\perp l'$,并延长使$C_1S = C_2S$,得点$C_2$;
顺次连接$A_2$,$B_2$,$C_2$,得到$\triangle A_2B_2C_2$。
3. 观察发现:
$\triangle ABC$与$\triangle A_2B_2C_2$关于点$($两平行线$l$,$l'$中心对称(或$\triangle ABC$与$\triangle A_2B_2C_2$形状、大小相同,方向相反,且对应点所连线段平行于$l$与$l'$的间距中线或者由两次轴对称可知$\triangle ABC$与$\triangle A_2B_2C_2$成中心对称)。
查看更多完整答案,请扫码查看


