第98页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
1. 如图,下列各个图形中,能用∠1,∠AOB,∠O三种方法表示同一角的图形是 (
B
)
答案:
B
2. (2024秋·南通崇川区期末)如图,将一个三角板60°角的顶点与另一个三角板的直角顶点重合,∠1= 27°40',则∠2的度数是 (
A.27°40'
B.62°20'
C.57°40'
D.58°20'
C
)A.27°40'
B.62°20'
C.57°40'
D.58°20'
答案:
C
3. 如图,图中一共有
7
个角,分别为∠B、∠ADB、∠ADC、∠C、∠BAD、∠DAC、∠BAC
.
答案:
7 ∠B、∠ADB、∠ADC、∠C、∠BAD、∠DAC、∠BAC
4. 如图:
(1)∠AOC= ∠
(2)∠BOC= ∠
(3)若∠AOC= ∠BOD,则∠AOB= ∠
(1)∠AOC= ∠
AOB
+∠BOC
= ∠AOD
-∠COD
;(2)∠BOC= ∠
AOC
-∠AOB
= ∠BOD
-∠COD
;(3)若∠AOC= ∠BOD,则∠AOB= ∠
COD
.
答案:
(1)AOB BOC AOD COD;
(2)AOC AOB BOD COD;
(3)COD
(1)AOB BOC AOD COD;
(2)AOC AOB BOD COD;
(3)COD
5. 计算:
(1)90°-35°40'17''=
(2)46.27°=
(3)21°18'×6=
(1)90°-35°40'17''=
54°19′43″
;(2)46.27°=
46
°16
'12
'';(3)21°18'×6=
127
°48
'.
答案:
(1)54°19′43″;
(2)46 16 12;
(3)127 48
(1)54°19′43″;
(2)46 16 12;
(3)127 48
6. 如图:
(1)用“<”把∠AOD、∠BOD、∠COD 连接起来;
(2)借助三角尺,估计∠AOB、∠BOC 和∠COD 的大小;
(3)∠AOD 等于哪两个角的和?
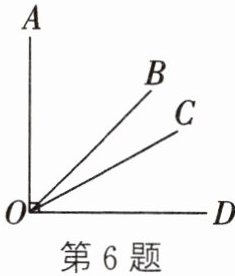
(1)用“<”把∠AOD、∠BOD、∠COD 连接起来;
(2)借助三角尺,估计∠AOB、∠BOC 和∠COD 的大小;
(3)∠AOD 等于哪两个角的和?

答案:
(1)∠COD<∠BOD<∠AOD;
(2)∠AOB=45°,∠BOC=15°,∠COD=30°;
(3)∠AOD=∠AOB+∠BOD=∠AOC+∠COD
(1)∠COD<∠BOD<∠AOD;
(2)∠AOB=45°,∠BOC=15°,∠COD=30°;
(3)∠AOD=∠AOB+∠BOD=∠AOC+∠COD
7. 若∠A= 20°18',∠B= 20°15'30'',∠C= 20.25°,则 (
A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
A
)A.∠A>∠B>∠C
B.∠B>∠A>∠C
C.∠A>∠C>∠B
D.∠C>∠A>∠B
答案:
A
查看更多完整答案,请扫码查看


