《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

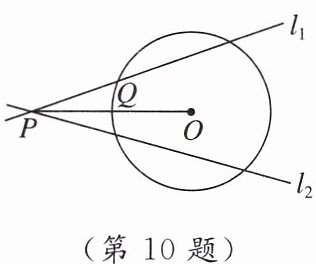
10. [2025 嘉兴期末] 如图,点$P为\odot O$外一点,连结$OP交\odot O于点Q$,且$PQ = OQ$,经过点$P的直线l_{1}$,$l_{2}都与\odot O$有公共点,则$l_{1}与l_{2}所成的锐角\alpha$的取值范围是( )\nA. $0^{\circ}\leqslant\alpha\leqslant30^{\circ}$\nB. $0^{\circ}\leqslant\alpha\leqslant45^{\circ}$\nC. $0^{\circ}\leqslant\alpha\leqslant60^{\circ}$\nD. $0^{\circ}\leqslant\alpha\leqslant90^{\circ}$\n[img]
-

答案：
10.C　　[点拨]如图,当直线$l_1$,$l_2$都与$\odot O$相切时,过点O作$OA⊥$直线$l_1$,则$OA=OQ$.
∵$OQ=PQ$,
　　　　　　　　　　　　　　　　　　　
∴易得$\angle OPA=30^{\circ}$.
　　设直线$l_2$与$\odot O$相切于点B,则同理可得$\angle OPB=30^{\circ}$.
∴$\angle APB=60^{\circ}$.
∴$0^{\circ}\leq \alpha \leq 60^{\circ}$.

11. 如图,在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\cos A= \frac{4}{5}$,$CD为AB$边上的中线,$CD = 5$,以点$B$为圆心,$r为半径作\odot B$。如果$\odot B与中线CD$有且只有一个公共点,那么$\odot B的半径r$的取值范围为______$5＜r\leq 6$或$r=\frac{24}{5}$。

答案： 11.$5＜r\leq 6$或$r=\frac{24}{5}$　　[点拨]在$Rt\triangle ABC$中,
　　$\angle ACB=90^{\circ}$,$CD$为AB边上的中线,$CD=5$,
∴$AB=10$,$BD=CD=5$.
∵$\cos A=\frac{AC}{AB}=\frac{4}{5}$,
∴$AC=8$.
∴$BC=\sqrt{AB^2 - AC^2}=\sqrt{10^2 - 8^2}=6$.
∴$CD$边上的高为$6×8×\frac{1}{2}×\frac{1}{2}×2÷5=\frac{24}{5}$.
∵$\odot B$与中线$CD$有且只有一个公共点，
∴$\odot B$的半径$r$的取值范围为$5＜r\leq 6$或$r=\frac{24}{5}$.

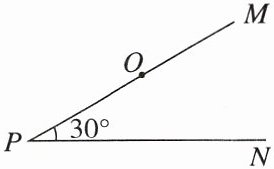
12. 如图,$PM$,$PN是两条夹角为30^{\circ}$的笔直的公路,在距离点$P为8千米的点O$处,有一个特定通讯设备信号发射中心,在它的周围$5$千米(包括$5$千米)范围内该特定通讯设备才可以正常使用,小王早上$8:00从点P$出发,乘坐速度为每小时$30千米的汽车向PN$方向行进,小王什么时刻使用该通讯设备为好？通讯时间最多可以是几分钟？(结果精确到分,$\sqrt{3}\approx1.7$)\n[img]

答案：
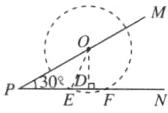
12.[解]如图,过O作$OD⊥PN$,交$PN$于D.以点O为圆心,5为半径作圆，与$PN$相交于点E,F,连接$OE$.
　　在$Rt\triangle POD$中,$\angle P=30^{\circ}$,
∴$OD=8×\sin 30^{\circ}=4$(千米),
∵$OE=5$千米,
∴$DE=3$千米,
∴$EF=6$千米,
∵$PD=\sqrt{PO^2 - DO^2}=\sqrt{64 - 16}=4\sqrt{3}$(千米)≈$6.8$千米,
　　　　　　　　　　　　　　　　　　
∴$PE=PD - DE≈3.8$千米,
∴$3.8÷30×60≈8$(分钟),
∴到$8:08$使用该通讯设备为好,此时，通讯时间可持续最长，最长通讯时间为$6÷30×60=12$(分钟),
答:到$8:08$使用该通讯设备为好，通讯时间最多可以是12分钟

13. 【新知】19世纪英国著名文学家和历史学家卡莱尔给出了一元二次方程$x^{2}+bx + c = 0$的几何解法：如图①,在平面直角坐标系中,已知点$A(0,1)$,$B(-b,c)$,以$AB为直径作\odot P$。若$\odot P交x轴于点M(m,0)$,$N(n,0)$,则$m$,$n为方程x^{2}+bx + c = 0$的两个实数根。\n【探究】(1)由勾股定理得$AM^{2}= 1^{2}+m^{2}$,$BM^{2}= c^{2}+(-b - m)^{2}$,$AB^{2}= (1 - c)^{2}+b^{2}$。在$Rt\triangle ABM$中,$AM^{2}+BM^{2}= AB^{2}$,所以$1^{2}+m^{2}+c^{2}+(-b - m)^{2}= (1 - c)^{2}+b^{2}$。化简得$m^{2}+bm + c = 0$。同理可得______。所以$m$,$n为方程x^{2}+bx + c = 0$的两个实数根；\n【运用】(2)在图②中的$x轴上画出以方程x^{2}-3x - 2 = 0两根为横坐标的点M$,$N$；
- (3)已知点$A(0,1)$,$B(6,9)$,以$AB为直径作\odot C$。判断$\odot C与x$轴的位置关系,并说明理由；
- 【拓展】(4)在平面直角坐标系中,已知两点$A(0,a)$,$B(-b,c)$,若以$AB为直径的圆与x轴有两个交点M$,$N$,则以点$M$,$N$的横坐标为根的一元二次方程是______。\n[img]
 

答案：
13.[解]
(1)$n^2+bn+c=0$　　[点拨]连接$AN$,$BN$,则$AN^2=1^2+n^2$,$BN^2=c^2+(−b−n)^2$,$AB^2=(1−c)^2+b^2$,在$Rt\triangle ABN$中,$AN^2+BN^2=AB^2$,
∴$1^2+n^2+c^2+(−b−n)^2=(1−c)^2+b^2$,
　　化简得$n^2+bn+c=0$.
(2)先在坐标系内找到点$A(0,1)$,$B(3,−2)$,连接$AB$,
　　　　　　　　
　分别以$A$,$B$为圆心,以大于$\frac{1}{2}AB$长为半径画弧，连接两弧的交点与$AB$交于点$P$,
　　以点$P$为圆心,以$AB$为直径画$\odot P$,$\odot P$与$x$轴的交点即为点$M$,$N$.如图所示,
(3)$\odot C$与$x$轴相切.理由:
　　由题意得方程为$x^2−6x+9=0$.
∵$\Delta =b^2−4ac=(−6)^2−4×1×9=0$,
∴方程$x^2−6x+9=0$有两个相等的实数根.
∴$\odot C$与$x$轴只有一个交点,即$\odot C$与$x$轴相切.
(4)$x^2+bx+ac=0$