《2025年综合应用创新题典中点九年级数学全一册浙教版浙江专版》

变式3-1 如图,D为△ABC内一点,E为△ABC外一点,且∠ABC= ∠DBE,∠3= ∠4. 求证：
(1)△ABD∽△CBE.
(2)△ABC∽△DBE.

答案：
(1)【证明】
∵∠ABC=∠DBE,
∴∠1=∠2.又
∵∠3=∠4,
∴△ABD∽△CBE.
(2)【证明】
∵△ABD∽△CBE,
∴$\frac{AB}{BC}=\frac{BD}{BE}$,
∴$\frac{AB}{BD}=\frac{BC}{BE}$.又
∵∠ABC=∠DBE,
∴△ABC∽△DBE.

变式3-2 如图,正方形ABCD和正方形BHGF,其中D,G,F三点共线,延长BG交CD于E,连结AH.
(1)求证：△EDG∽△EBD；
(2)不难证明：△BHA∽△BGD,因此$\frac{DG}{AH}$的值为$\sqrt{2}$.

答案：
(1)【证明】四边形ABCD和BHGF是正方形,
∴∠BDE=∠FGB=45°,
∴∠BDG+∠GDE=45°,∠BDG+∠DBG=∠DGE=∠BGF=45°.
∴∠GDE=∠DBG.
∵∠DEG=∠BED,
∴△EDG∽△EBD.
(2)$\sqrt{2}$【点拨】
∵四边形ABCD是正方形，四边形BHGF是正方形，
∴△ABD是等腰直角三角形，△HBG是等腰直角三角形，
∴$\frac{BD}{AB}=\frac{BG}{BH}=\sqrt{2}$，∠ABH=45°−∠DBH=∠GBD,
∴△BHA∽△BGD,
∴$\frac{DG}{AH}=\frac{BD}{AB}=\sqrt{2}$.

例4 如图,在矩形ABCD中,AB= 4,BC= 10,点E,F,M分别在AB,BC,AD上,∠EMF= 90°,AM= 2,当BE+BF= 9时,求四边形MEBF的面积.

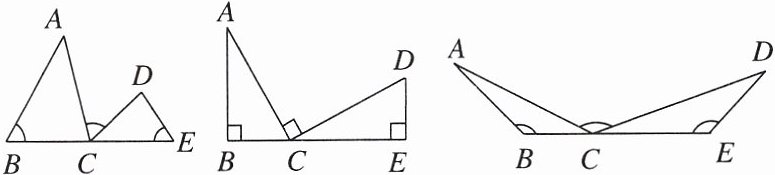
方法点拨：如图,点C在边BE上,若∠B= ∠ACD= ∠E,则△ABC∽△CED.

答案： 【解】如图,过点F作FH⊥AD于点H,由题意得∠A=∠EMF=∠FHM=90°,
∴∠AEM+∠AME=90°,∠FMH+∠AME=90°.
∴∠AEM=∠FMH.
∴△AME∽△HFM.
∴$\frac{AE}{MH}=\frac{AM}{HF}$.
∵在矩形ABCD中,∠A=∠B=90°,
∴四边形ABFH是矩形.
∴HF=AB=4,BF=AH=AM+MH.
∵AM=2,BE+BF=9,
∴BE+2+MH=9.
∴MH=7−BE.
∴$\frac{4−BE}{7−BE}=\frac{2}{4}$,解得BE=1,
∴MH=6,AE=AB−BE=3,BF=8.
∵四边形MEBF的面积=矩形ABFH的面积−S△AME−S△MHF,
∴四边形MEBF的面积=4×8−$\frac{1}{2}$×2×3−$\frac{1}{2}$×6×4=17.

变式4-1 如图,在△ABC中,AB= AC,点E在边BC上移动(点E不与点B,C重合),点D,F分别在边AB,AC上,且满足∠DEF= ∠B.
(1)求证：△BDE∽△CEF；
(2)当点E移动到BC的中点时,求证：FE平分∠DFC.

答案：
(1)【证明】
∵AB=AC,
∴∠B=∠C.
∵∠BDE=180°−∠B−∠DEB,∠CEF=180°−∠DEF−∠DEB,且∠DEF=∠B,
∴∠BDE=∠CEF.
∴△BDE∽△CEF.
(2)【证明】
∵△BDE∽△CEF,
∴$\frac{BE}{CF}=\frac{DE}{EF}$.
∵点E是BC的中点,
∴BE=CE.
∴$\frac{CE}{CF}=\frac{DE}{EF}$,
∴$\frac{CE}{DE}=\frac{CF}{EF}$.又易知∠DEF=∠C,
∴△DEF∽△ECF.
∴∠DFE=∠EFC.
∴FE平分∠DFC.