第62页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
12. 利用互余的两个角的正弦和余弦的关系,比较下列正弦值和余弦值的大小:$\sin10^{\circ}$,$\cos30^{\circ}$,$\sin50^{\circ}$,$\cos70^{\circ}$。
答案:
12.[解]cos30° = sin60°,cos70° = sin20°.
∵sin60°>sin50°>sin20°>sin10°,
∴cos30°>sin50°>cos70°>sin10°.
∵sin60°>sin50°>sin20°>sin10°,
∴cos30°>sin50°>cos70°>sin10°.
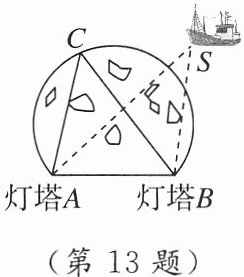
13. [2025杭州模拟] 如图,有一个弓形的暗礁区,弓形所含的圆周角$\angle C = 50^{\circ}$,船在航行时,为保证不进入暗礁区,则船到两个灯塔$A$,$B的张角\angle ASB$应满足的条件是(
A.$\sin\angle ASB > \sin25^{\circ}$
B.$\sin\angle ASB > \sin50^{\circ}$
C.$\tan\angle ASB > \tan50^{\circ}$
D.$\cos\angle ASB > \cos50^{\circ}$
D
)
A.$\sin\angle ASB > \sin25^{\circ}$
B.$\sin\angle ASB > \sin50^{\circ}$
C.$\tan\angle ASB > \tan50^{\circ}$
D.$\cos\angle ASB > \cos50^{\circ}$
答案:
13.D [点拨]如图,设AS交弓形于点E,连结EB,由圆周角定理知,∠AEB = ∠C = 50°,
∵∠AEB是△SEB的一个外角,
∴∠AEB>∠S,当∠S<50°时船不进入暗礁区,
∴张角∠ASB应满足的条件是∠ASB<50°,
∴cos∠ASB>cos50°.
∵∠AEB是△SEB的一个外角,
∴∠AEB>∠S,当∠S<50°时船不进入暗礁区,
∴张角∠ASB应满足的条件是∠ASB<50°,
∴cos∠ASB>cos50°.
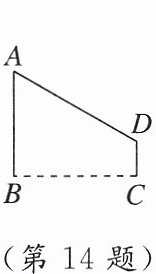
14. 如图,某工厂为了提升生产过程中所产生废气的净化效率,需在气体净化设备上增加一条管道$A - D - C$,已知$DC\perp BC$,$AB\perp BC$,$\angle A = 60^{\circ}$,$AB = 11\mathrm{m}$,$CD = 4\mathrm{m}$,则管道$A - D - C$的总长为______$\mathrm{m}$。

18
答案:
14.18
15. 情境题 生活应用 在坐标平面上,机器人能根据指令$[s,\alpha](s\geq0,0^{\circ}<\alpha < 180^{\circ})$完成下列动作:先原地顺时针旋转角度$\alpha$,再朝其对面方向沿直线行走距离$s$。
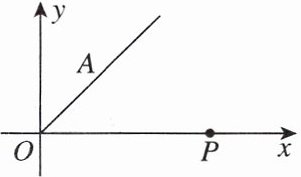
(1) 如图,若机器人在直角坐标系的原点,且面对$y$轴的正方向,现要使其移动到点$A(2,2)$,则给机器人发出的指令应是什么?
(2) 机器人在完成上述指令后,发现在$P(6,0)$处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球。(角度精确到度;参考数据:$\sin49^{\circ}\approx0.75$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$)
(1) 如图,若机器人在直角坐标系的原点,且面对$y$轴的正方向,现要使其移动到点$A(2,2)$,则给机器人发出的指令应是什么?
(2) 机器人在完成上述指令后,发现在$P(6,0)$处有一小球正向坐标原点做匀速直线运动,已知小球滚动的速度与机器人行走的速度相同,若忽略机器人原地旋转的时间,请你给机器人发一个指令,使它能最快截住小球。(角度精确到度;参考数据:$\sin49^{\circ}\approx0.75$,$\cos37^{\circ}\approx0.80$,$\tan37^{\circ}\approx0.75$)

答案:
15.[解]
(1)如图,过点A作AB⊥x轴.
∵A(2,2),
∴OB = 2,AB = 2,
∴易得OA = 2√2,∠AOB = 45°,
∴给机器人发出的指令为[2√2,45°].
(2)
∵P(6,0),
∴OP = 6.如图,在x轴上找一点C,连结AC,使AC = PC,设PC = x,则BC = OP - OB - PC = 4 - x,在Rt△ABC中,2²+(4 - x)² = x²,解得x = 2.5.又
∵tan∠BAC = BC/AB = (4 - 2.5)/2 = 0.75,
∴∠BAC≈37°.易知∠OAB = 45°,
∴∠OAC≈37° + 45° = 82°,
∴∠DAC≈180° - 82° = 98°,
∴给机器人发的指令为[2.5,98°].
(1)如图,过点A作AB⊥x轴.
∵A(2,2),
∴OB = 2,AB = 2,
∴易得OA = 2√2,∠AOB = 45°,
∴给机器人发出的指令为[2√2,45°].
(2)
∵P(6,0),
∴OP = 6.如图,在x轴上找一点C,连结AC,使AC = PC,设PC = x,则BC = OP - OB - PC = 4 - x,在Rt△ABC中,2²+(4 - x)² = x²,解得x = 2.5.又
∵tan∠BAC = BC/AB = (4 - 2.5)/2 = 0.75,
∴∠BAC≈37°.易知∠OAB = 45°,
∴∠OAC≈37° + 45° = 82°,
∴∠DAC≈180° - 82° = 98°,
∴给机器人发的指令为[2.5,98°].
16. 新视角 猜想验证题
(1) 通过计算(可用计算器),比较下列各组数的大小,并提出你的猜想:
①$\sin30^{\circ}$
②$\sin36^{\circ}$
③$\sin45^{\circ}$
④$\sin60^{\circ}$
⑤$\sin80^{\circ}$
猜想:已知$0^{\circ}<\alpha < 45^{\circ}$,则$\sin2\alpha$
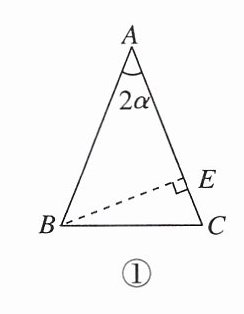
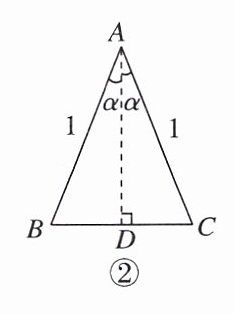
(2) 如图①,图②,在$\triangle ABC$中,$AB = AC = 1$,$\angle BAC = 2\alpha$,请根据提示,利用面积方法验证结论。
(1) 通过计算(可用计算器),比较下列各组数的大小,并提出你的猜想:
①$\sin30^{\circ}$
=
$2\sin15^{\circ}\cos15^{\circ}$;②$\sin36^{\circ}$
=
$2\sin18^{\circ}\cos18^{\circ}$;③$\sin45^{\circ}$
=
$2\sin22.5^{\circ}\cos22.5^{\circ}$;④$\sin60^{\circ}$
=
$2\sin30^{\circ}\cos30^{\circ}$;⑤$\sin80^{\circ}$
=
$2\sin40^{\circ}\cos40^{\circ}$。猜想:已知$0^{\circ}<\alpha < 45^{\circ}$,则$\sin2\alpha$
=
$2\sin\alpha\cos\alpha$(填“$>$”“$<$”或“$=$”)。(2) 如图①,图②,在$\triangle ABC$中,$AB = AC = 1$,$\angle BAC = 2\alpha$,请根据提示,利用面积方法验证结论。


答案:
16.[解]
(1)①= ②= ③= ④= ⑤= =
(2)
∵题图②中,AB = AC,AD⊥BC,
∴BC = 2BD.
∵题图①中△ABC的面积为1/2AC·BE = 1/2×1×1×sin2α = 1/2sin2α,题图②中△ABC的面积为1/2BC·AD = 1/2×2BD·AD = 1/2×2×1×sinα×1×cosα = sinαcosα,
∴sin2α = 2sinαcosα.
(1)①= ②= ③= ④= ⑤= =
(2)
∵题图②中,AB = AC,AD⊥BC,
∴BC = 2BD.
∵题图①中△ABC的面积为1/2AC·BE = 1/2×1×1×sin2α = 1/2sin2α,题图②中△ABC的面积为1/2BC·AD = 1/2×2BD·AD = 1/2×2×1×sinα×1×cosα = sinαcosα,
∴sin2α = 2sinαcosα.
查看更多完整答案,请扫码查看


