第35页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
11. 新趋势数学文化我国魏晋时期数学家刘徽在《九章算术注》中提到了著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算,指出“割之弥细,所失弥少.割之又割,以至于不可割,则与圆周合体,而无所失矣”。“割圆术”孕育了微积分思想,他用这种思想得到了圆周率$\pi$的近似值为3.1416。如图,$\odot O$的半径为1,运用“割圆术”,以圆内接正六边形的面积近似估计$\odot O$的面积,可得$\pi的估计值为\frac{3\sqrt{3}}{2}$,若用圆内接正八边形作近似估计,可得$\pi$的估计值为(
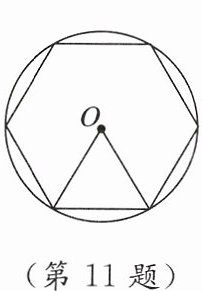
A.$\sqrt{3}$
B.$2\sqrt{2}$
C.3
D.$2\sqrt{3}$
B
)
A.$\sqrt{3}$
B.$2\sqrt{2}$
C.3
D.$2\sqrt{3}$
答案:
B
12. 如图,用若干个全等的正五边形排成圆环状,图中所示的是其中3个正五边形的位置,要完成这一圆环排列,共需要正五边形
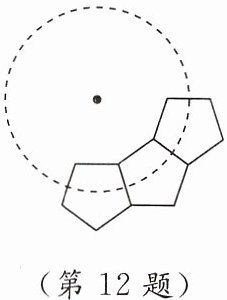
10
个。
答案:
10
13. 如图,六边形$ABCDEF是\odot O$的内接正六边形,设正六边形$ABCDEF的面积为S_1$,$\triangle ACE的面积为S_2$,则$\frac{S_1}{S_2}= $____。


答案:
2 [点拨]如图,连结OA,OC,OE.
∵六边形ABCDEF是$\odot O$的内接正六边形,
∴AC = AE = CE,
∴△ACE是$\odot O$的内接正三角形.
∵∠B = 120°,AB = BC,
∴∠BAC = ∠BCA = $\frac{1}{2}$(180° - ∠B) = 30°,
∵∠CAE = 60°,
∴∠OAC = ∠OAE = 30°,
∴∠BAC = ∠OAC = 30°,同理可得,∠BCA = ∠OCA = 30°.又
∵AC = AC,
∴△BAC ≌ △OAC(ASA),
∴$S_{△ABC}$ = $S_{△AOC}$.由圆和正六边形的性质可得,$S_{△BAC}$ = $S_{△AFE}$ = $S_{△CDE}$,由圆和正三角形的性质可得,$S_{△AOC}$ = $S_{△AOE}$ = $S_{△COE}$.
∵$S_{1}$ = $S_{△BAC}$ + $S_{△AFE}$ + $S_{△CDE}$ + $S_{△AOC}$ + $S_{△AOE}$ + $S_{△COE}$ = 2($S_{△AOC}$ + $S_{△AOE}$ + $S_{△COE}$) = 2$S_{2}$,
∴$\frac{S_{1}}{S_{2}}$ = 2.

2 [点拨]如图,连结OA,OC,OE.
∵六边形ABCDEF是$\odot O$的内接正六边形,
∴AC = AE = CE,
∴△ACE是$\odot O$的内接正三角形.
∵∠B = 120°,AB = BC,
∴∠BAC = ∠BCA = $\frac{1}{2}$(180° - ∠B) = 30°,
∵∠CAE = 60°,
∴∠OAC = ∠OAE = 30°,
∴∠BAC = ∠OAC = 30°,同理可得,∠BCA = ∠OCA = 30°.又
∵AC = AC,
∴△BAC ≌ △OAC(ASA),
∴$S_{△ABC}$ = $S_{△AOC}$.由圆和正六边形的性质可得,$S_{△BAC}$ = $S_{△AFE}$ = $S_{△CDE}$,由圆和正三角形的性质可得,$S_{△AOC}$ = $S_{△AOE}$ = $S_{△COE}$.
∵$S_{1}$ = $S_{△BAC}$ + $S_{△AFE}$ + $S_{△CDE}$ + $S_{△AOC}$ + $S_{△AOE}$ + $S_{△COE}$ = 2($S_{△AOC}$ + $S_{△AOE}$ + $S_{△COE}$) = 2$S_{2}$,
∴$\frac{S_{1}}{S_{2}}$ = 2.

14. 作图与证明:如图,已知$\odot O和\odot O上的一点A$,请回答下列问题:
(1)作$\odot O的内接正六边形ABCDEF$。
(2)连结$BF$,$CE$,判断四边形$BCEF$的形状并加以证明。

(1)作$\odot O的内接正六边形ABCDEF$。
(2)连结$BF$,$CE$,判断四边形$BCEF$的形状并加以证明。

答案:
[解]
(1)如图①所示.

(2)四边形BCEF是矩形.证明如下:
如图②,
∵六边形ABCDEF是正六边形,
∴∠EDC = ∠FED = 120°,AB = AF = DE = DC = FE = BC,
∴$\widehat{AB}$ = $\widehat{AF}$ = $\widehat{DE}$ = $\widehat{DC}$,
∴$\widehat{BF}$ = $\widehat{CE}$,
∴BF = CE,
∴四边形BCEF是平行四边形.
∵DE = DC,∠EDC = 120°,
∴∠DEC = ∠DCE = 30°,
∴∠CEF = ∠FED - ∠DEC = 90°,
∴▱BCEF是矩形.
[解]
(1)如图①所示.

(2)四边形BCEF是矩形.证明如下:
如图②,
∵六边形ABCDEF是正六边形,
∴∠EDC = ∠FED = 120°,AB = AF = DE = DC = FE = BC,
∴$\widehat{AB}$ = $\widehat{AF}$ = $\widehat{DE}$ = $\widehat{DC}$,
∴$\widehat{BF}$ = $\widehat{CE}$,
∴BF = CE,
∴四边形BCEF是平行四边形.
∵DE = DC,∠EDC = 120°,
∴∠DEC = ∠DCE = 30°,
∴∠CEF = ∠FED - ∠DEC = 90°,
∴▱BCEF是矩形.
15. 新考法归纳法如图,$M$,$N分别是\odot O的内接正三角形ABC$,正方形$ABCD$,正五边形$ABCDE$,…$$,正$n边形ABCDEFG…的边AB$,$BC$上的点,且$BM = CN$,连结$OM$,$ON$。
(1)求图①中$\angle MON$的度数。
(2)图②中$\angle MON$的度数是____,图③中$\angle MON$的度数是____。
(3)$\angle MON的度数与正n边形的边数n$的关系是____。

(1)求图①中$\angle MON$的度数。
(2)图②中$\angle MON$的度数是____,图③中$\angle MON$的度数是____。
(3)$\angle MON的度数与正n边形的边数n$的关系是____。

答案:
[解]
(1)如图①,连结OB,OC,则OC = OB.
∵△ABC是$\odot O$的内接正三角形,
∴∠BOC = $\frac{360^{\circ}}{3}$ = 120°.
由题意易知∠OBM = $\frac{1}{2}$∠ABC = 30°,∠OCN = $\frac{1}{2}$∠ACB = 30°,
∴∠OBM = ∠OCN.
在△OMB和△ONC中,$\begin{cases}BM = CN\\∠OBM = ∠OCN\\OB = OC\end{cases}$
∴△OMB ≌ △ONC,
∴∠BOM = ∠CON,
∴∠MON = ∠BON + ∠BOM = ∠BON + ∠CON = ∠BOC = 120°.

(2)$90^{\circ};72^{\circ}$ [点拨]如图②,连结OB,OC.
∵四边形ABCD是$\odot O$的内接正方形,
∴∠BOC = $\frac{360^{\circ}}{4}$ = 90°.
同
(1)的方法可得∠MON = ∠BOC = 90°;
如图③,连结OB,OC,
∵五边形ABCDE是$\odot O$的内接正五边形,
∴∠BOC = $\frac{360^{\circ}}{5}$ = 72°,
同
(1)的方法可得∠MON = ∠BOC = 72°.
(3)∠MON = $\frac{360^{\circ}}{n}$
[解]
(1)如图①,连结OB,OC,则OC = OB.
∵△ABC是$\odot O$的内接正三角形,
∴∠BOC = $\frac{360^{\circ}}{3}$ = 120°.
由题意易知∠OBM = $\frac{1}{2}$∠ABC = 30°,∠OCN = $\frac{1}{2}$∠ACB = 30°,
∴∠OBM = ∠OCN.
在△OMB和△ONC中,$\begin{cases}BM = CN\\∠OBM = ∠OCN\\OB = OC\end{cases}$
∴△OMB ≌ △ONC,
∴∠BOM = ∠CON,
∴∠MON = ∠BON + ∠BOM = ∠BON + ∠CON = ∠BOC = 120°.

(2)$90^{\circ};72^{\circ}$ [点拨]如图②,连结OB,OC.
∵四边形ABCD是$\odot O$的内接正方形,
∴∠BOC = $\frac{360^{\circ}}{4}$ = 90°.
同
(1)的方法可得∠MON = ∠BOC = 90°;
如图③,连结OB,OC,
∵五边形ABCDE是$\odot O$的内接正五边形,
∴∠BOC = $\frac{360^{\circ}}{5}$ = 72°,
同
(1)的方法可得∠MON = ∠BOC = 72°.
(3)∠MON = $\frac{360^{\circ}}{n}$
查看更多完整答案,请扫码查看


