第45页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
1. 平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形
相似
.
答案:
相似
2. 有两个角
对应相等
的两个三角形相似.
答案:
对应相等
1. 如图,在$△ABC$中,$DE// BC$,则下列比例式一定正确的是(
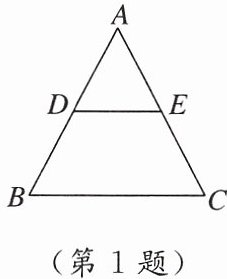
A.$\frac {DE}{BC}= \frac {AD}{DB}$
B.$\frac {AD}{AB}= \frac {DE}{BC}$
C.$\frac {AD}{EC}= \frac {AE}{DB}$
D.$\frac {DE}{BC}= \frac {EC}{AC}$
B
)
A.$\frac {DE}{BC}= \frac {AD}{DB}$
B.$\frac {AD}{AB}= \frac {DE}{BC}$
C.$\frac {AD}{EC}= \frac {AE}{DB}$
D.$\frac {DE}{BC}= \frac {EC}{AC}$
答案:
B
2. 如图,在$△ABC$中,$D,E分别是AB,AC$上的点,$DE// BC,\frac {AD}{AB}= \frac {1}{3}$.若$DE= 2$,则$BC$的长是(

A.3
B.4
C.6
D.8
C
)
A.3
B.4
C.6
D.8
答案:
C
3. 新考向 知识情境化 如图,在$△ABC$中,$∠ABC= 90^{\circ },∠A= 60^{\circ }$,直尺的一边与$BC$重合,另一边分别交$AB,AC于点D,E$.点$B,C,D,E$处的读数分别为15,12,0,1,则直尺宽$BD$的长为____
$\frac{2\sqrt{3}}{3}$
.zyjl.cn/pic18/2025-08-16/d8b01838bf98a9e37c4b2860d19a5253.jpg?x-oss-process=image/crop,x_308,y_2185,w_330,h_195">
答案:
$\frac{2\sqrt{3}}{3}$cm
4. 下列各组图形中,可能不相似的是(
A.各有一个角是$45^{\circ }$的两个等腰三角形
B.各有一个角是$60^{\circ }$的两个等腰三角形
C.各有一个角是$90^{\circ }$的两个等腰三角形
D.各有一个角是$105^{\circ }$的两个等腰三角形
A
)A.各有一个角是$45^{\circ }$的两个等腰三角形
B.各有一个角是$60^{\circ }$的两个等腰三角形
C.各有一个角是$90^{\circ }$的两个等腰三角形
D.各有一个角是$105^{\circ }$的两个等腰三角形
答案:
A
5. 如图,$AB// DC,AC交BD于点O$.若$\frac {AO}{CO}= \frac {3}{5},BO= 6$,则$DO$的长为(
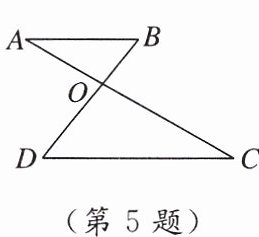
A.$\frac {18}{5}$
B.6
C.10
D.12
C
)
A.$\frac {18}{5}$
B.6
C.10
D.12
答案:
C
6. 如图,$D,E分别是△ABC边AB,AC$上的点,$∠ADE= ∠ACB$.若$AD= 2,AB= 6,AC= 4$,则$AE$的长为(

A.1
B.2
C.3
D.4
C
)
A.1
B.2
C.3
D.4
答案:
C
7. 如图,已知$∠1= ∠2$,补充一个条件:
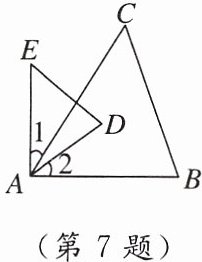
∠E=∠C(答案不唯一)
(写出一个即可),可使$△ADE\backsim △ABC$.
答案:
∠E=∠C(答案不唯一)
8. 如图,$AE,BD相交于点C,BA⊥AE于点A,ED⊥BD于点D$.若$AC= 4,AB= 3,CD= 2$,则$DE= $
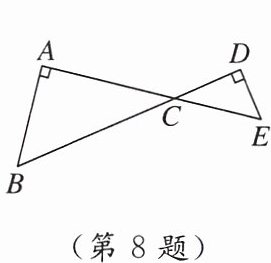
$\frac{3}{2}$
.
答案:
$\frac{3}{2}$
9. 如图,在平行四边形$ABCD$中,过点$A作AE⊥BC$,垂足为$E$,连结$DE,F为线段DE$上一点,连结$AF且∠1= ∠B$.求证:$△ADF\backsim △DEC$.
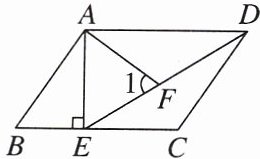

答案:
[证明]
∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD.
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD.
∴△ADF∽△DEC.
∵四边形ABCD是平行四边形,
∴AD//BC,AB//CD.
∴∠ADF=∠DEC,∠C+∠B=180°.
∵∠1=∠B,∠1+∠AFD=180°,
∴∠C=∠AFD.
∴△ADF∽△DEC.
查看更多完整答案,请扫码查看


