第12页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
例1 将二次函数 $ y = -(x - k)^2 + k + 1 $ 的图象向右平移1个单位,再向上平移2个单位后,顶点在直线 $ y = 2x + 2 $ 上,则 $ k $ 的值为(
A.2
B.1
C.0
D.-1
D
)A.2
B.1
C.0
D.-1
答案:
例1 D [点拨]
∵二次函数$y=-(x-k)^2+k+1$的图象的顶点坐标为$(k,k+1)$,
∴将$y=-(x-k)^2+k+1$的图象向右平移1个单位,再向上平移2个单位后,顶点坐标为$(k+1,k+3)$.根据题意,得$k+3=2(k+1)+2$,解得$k=-1$.
∵二次函数$y=-(x-k)^2+k+1$的图象的顶点坐标为$(k,k+1)$,
∴将$y=-(x-k)^2+k+1$的图象向右平移1个单位,再向上平移2个单位后,顶点坐标为$(k+1,k+3)$.根据题意,得$k+3=2(k+1)+2$,解得$k=-1$.
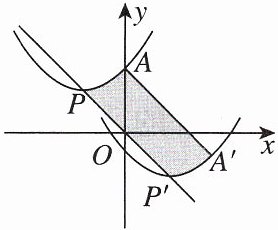
变式1-1 如图,抛物线的顶点为 $ P(-2, 2) $,与 $ y $ 轴交于点 $ A(0, 3) $,若平移该抛物线使其顶点 $ P $ 沿直线移动到点 $ P'(2, -2) $,点 $ A $ 的对应点为 $ A' $,则抛物线上 $ PA $ 段扫过的区域(阴影部分)的面积为______。

12
答案:
变式1 -1 12 [点拨]连结$AP,A'P'$,过点A作$AD\perp PP'$于点D.
由题意可得出$AP// A'P'$,$AP=A'P'$,
∴四边形$APP'A'$是平行四边形.
∵抛物线的顶点为$P(-2,2)$,与y轴交于点$A(0,3)$,平移该抛物线使其顶点P沿直线移动到点$P'(2,-2)$,
∴$PP'=\sqrt{[2-(-2)]^2+[(-2)-2]^2}=4\sqrt{2}$,$\angle AOD = 45^{\circ}$,$AO = 3$,
∴$\triangle AOD$是等腰直角三角形,
∴$AD = OD$.
∵$AD^2+OD^2=AO^2$,
∴$2AD^2=3^2$,
∴$AD=\frac{3\sqrt{2}}{2}$,
∴抛物线上PA段扫过的区域(阴影部分)的面积为$4\sqrt{2}×\frac{3\sqrt{2}}{2}=12$.
由题意可得出$AP// A'P'$,$AP=A'P'$,
∴四边形$APP'A'$是平行四边形.
∵抛物线的顶点为$P(-2,2)$,与y轴交于点$A(0,3)$,平移该抛物线使其顶点P沿直线移动到点$P'(2,-2)$,
∴$PP'=\sqrt{[2-(-2)]^2+[(-2)-2]^2}=4\sqrt{2}$,$\angle AOD = 45^{\circ}$,$AO = 3$,
∴$\triangle AOD$是等腰直角三角形,
∴$AD = OD$.
∵$AD^2+OD^2=AO^2$,
∴$2AD^2=3^2$,
∴$AD=\frac{3\sqrt{2}}{2}$,
∴抛物线上PA段扫过的区域(阴影部分)的面积为$4\sqrt{2}×\frac{3\sqrt{2}}{2}=12$.
例2 在同一平面直角坐标系中,若抛物线 $ y = -ax^2 + 3x - c $ 与 $ y = 2x^2 - 3x - c + a $ 关于 $ x $ 轴对称,则 $ a + 2c $ 的值为(
A.0
B.-4
C.4
D.-1
C
)A.0
B.-4
C.4
D.-1
答案:
例2 C [点拨]
∵抛物线$y=-ax^2+3x - c$关于x轴对称的抛物线的函数表达式为$y=ax^2-3x + c$,且抛物线$y=-ax^2+3x - c$与$y=2x^2-3x - c + a$关于x轴对称,
∴$\begin{cases}a = 2\\-c + a = c\end{cases}$,解得$\begin{cases}a = 2\\c = 1\end{cases}$.
∴$a + 2c = 2 + 2 = 4$.
∵抛物线$y=-ax^2+3x - c$关于x轴对称的抛物线的函数表达式为$y=ax^2-3x + c$,且抛物线$y=-ax^2+3x - c$与$y=2x^2-3x - c + a$关于x轴对称,
∴$\begin{cases}a = 2\\-c + a = c\end{cases}$,解得$\begin{cases}a = 2\\c = 1\end{cases}$.
∴$a + 2c = 2 + 2 = 4$.
变式2-1 新视角 新定义题 规定:如果两个函数的图象关于 $ y $ 轴对称,那么称这两个函数互为“$ Y $ 函数”。例如:函数 $ y = x + 3 $ 与 $ y = -x + 3 $ 互为“$ Y $ 函数”。若函数 $ y = \frac{k}{4}x^2 + (k - 1)x + k - 3 $ 的图象与 $ x $ 轴只有一个交点,则它的“$ Y $ 函数”图象与 $ x $ 轴的交点坐标为______
$(3,0)$或$(4,0)$
。
答案:
变式2 -1 $(3,0)$或$(4,0)$ [点拨]当$k = 0$时,函数的表达式为$y=-x - 3$,此时函数的图象与x轴只有一个交点,成立,令$y = 0$,得$0=-x - 3$,解得$x=-3$,
∴函数$y=-x - 3$的图象与x轴的交点坐标为$(-3,0)$.根据题意得,它的“Y函数”图象与x轴的交点坐标为$(3,0)$;
当$k\neq0$时,
∵函数$y=\frac{k}{4}x^2+(k - 1)x + k - 3$的图象与x轴只有一个交点,
∴对于方程$\frac{k}{4}x^2+(k - 1)x + k - 3 = 0$,有$(k - 1)^2-4×\frac{k}{4}×(k - 3)=0$,解得$k=-1$,
∴函数的表达式为$y=-\frac{1}{4}x^2-2x - 4$.
令$y = 0$,得$0=-\frac{1}{4}x^2-2x - 4$,解得$x_1=x_2=-4$.
∴函数$y=-\frac{1}{4}x^2-2x - 4$的图象与x轴的交点坐标为$(-4,0)$.
根据题意得,它的“Y函数”图象与x轴的交点坐标为$(4,0)$.综上所述,它的“Y函数”图象与x轴的交点坐标为$(3,0)$或$(4,0)$.
∴函数$y=-x - 3$的图象与x轴的交点坐标为$(-3,0)$.根据题意得,它的“Y函数”图象与x轴的交点坐标为$(3,0)$;
当$k\neq0$时,
∵函数$y=\frac{k}{4}x^2+(k - 1)x + k - 3$的图象与x轴只有一个交点,
∴对于方程$\frac{k}{4}x^2+(k - 1)x + k - 3 = 0$,有$(k - 1)^2-4×\frac{k}{4}×(k - 3)=0$,解得$k=-1$,
∴函数的表达式为$y=-\frac{1}{4}x^2-2x - 4$.
令$y = 0$,得$0=-\frac{1}{4}x^2-2x - 4$,解得$x_1=x_2=-4$.
∴函数$y=-\frac{1}{4}x^2-2x - 4$的图象与x轴的交点坐标为$(-4,0)$.
根据题意得,它的“Y函数”图象与x轴的交点坐标为$(4,0)$.综上所述,它的“Y函数”图象与x轴的交点坐标为$(3,0)$或$(4,0)$.
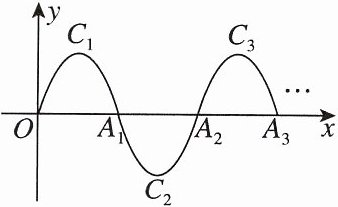
例3 如图,一段抛物线 $ y = -x(x - 3)(0 \leq x \leq 3) $,记为 $ C_1 $,它与 $ x $ 轴交于点 $ O, A_1 $;将 $ C_1 $ 绕点 $ A_1 $ 旋转 $ 180^\circ $ 得 $ C_2 $,交 $ x $ 轴于点 $ A_2 $;将 $ C_2 $ 绕点 $ A_2 $ 旋转 $ 180^\circ $ 得 $ C_3 $,交 $ x $ 轴于点 $ A_3 $;…;如此进行下去,若 $ P(40, m) $ 在其中一段抛物线上,则 $ m = $______
方法点拨:在解答二次函数图象的旋转问题时,需抓住函数图象形状、大小不变,只改变方向或位置这一关键点,进而解决问题。
-2
。
方法点拨:在解答二次函数图象的旋转问题时,需抓住函数图象形状、大小不变,只改变方向或位置这一关键点,进而解决问题。
答案:
例3 -2 [点拨]
∵一段抛物线$y=-x(x - 3)(0\leqslant x\leqslant 3)$,
∴图象与x轴的交点坐标为$(0,0)$,$(3,0)$.
∴将$C_1$绕点$A_1$旋转$180^{\circ}$得$C_2$,交x轴于点$A_2(6,0)$;
将$C_2$绕点$A_2$旋转$180^{\circ}$得$C_3$,交x轴于点$A_3(9,0)$;
如此进行下去,直至得$C_{14}$,$C_{14}$与x轴的交点坐标为$A_{13}(39,0)$,$A_{14}(42,0)$,且图象在x轴下方.
∴$C_{14}$的表达式为$y=(x - 39)(x - 42)$,
当$x = 40$时,$m=(40 - 39)(40 - 42)=-2$.
∵一段抛物线$y=-x(x - 3)(0\leqslant x\leqslant 3)$,
∴图象与x轴的交点坐标为$(0,0)$,$(3,0)$.
∴将$C_1$绕点$A_1$旋转$180^{\circ}$得$C_2$,交x轴于点$A_2(6,0)$;
将$C_2$绕点$A_2$旋转$180^{\circ}$得$C_3$,交x轴于点$A_3(9,0)$;
如此进行下去,直至得$C_{14}$,$C_{14}$与x轴的交点坐标为$A_{13}(39,0)$,$A_{14}(42,0)$,且图象在x轴下方.
∴$C_{14}$的表达式为$y=(x - 39)(x - 42)$,
当$x = 40$时,$m=(40 - 39)(40 - 42)=-2$.
变式3-1 如果二次函数 $ y_1 $ 的图象的顶点在二次函数 $ y_2 $ 的图象上,同时二次函数 $ y_2 $ 的图象的顶点在二次函数 $ y_1 $ 的图象上,那么我们称这两个函数互为“顶点相容函数”。
(1) 若二次函数 $ y_1 = x^2 - 2x - 3 $ 与二次函数 $ y_2 = -x^2 + bx - 7 $ 互为“顶点相容函数”,则 $ b = $______;
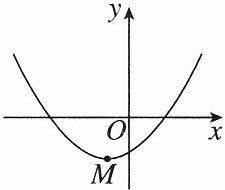
(2) 如图,已知二次函数 $ y_1 = \frac{1}{4}(x + 1)^2 - 2 $ 的图象的顶点为 $ M $,点 $ P $ 是 $ x $ 轴正半轴上的一个动点,将二次函数 $ y_1 $ 的图象绕点 $ P $ 旋转 $ 180^\circ $ 得到一个新的二次函数 $ y_2 $ 的图象,旋转前后的两个函数互为“顶点相容函数”,且 $ y_2 $ 的图象的顶点为 $ N $。求二次函数 $ y_2 $ 的表达式。
(1) 若二次函数 $ y_1 = x^2 - 2x - 3 $ 与二次函数 $ y_2 = -x^2 + bx - 7 $ 互为“顶点相容函数”,则 $ b = $______;
(2) 如图,已知二次函数 $ y_1 = \frac{1}{4}(x + 1)^2 - 2 $ 的图象的顶点为 $ M $,点 $ P $ 是 $ x $ 轴正半轴上的一个动点,将二次函数 $ y_1 $ 的图象绕点 $ P $ 旋转 $ 180^\circ $ 得到一个新的二次函数 $ y_2 $ 的图象,旋转前后的两个函数互为“顶点相容函数”,且 $ y_2 $ 的图象的顶点为 $ N $。求二次函数 $ y_2 $ 的表达式。

答案:
变式3 -1 [解]
(1)4
(2)
∵旋转前后的两个函数互为“顶点相容函数”,
∴二次函数$y_2$图象的顶点N必在二次函数$y_1=\frac{1}{4}(x + 1)^2-2$的图象上,
∵二次函数$y_2$的图象是由二次函数$y_1=\frac{1}{4}(x + 1)^2-2$的图象绕点P旋转$180^{\circ}$得到的,
∴这两个函数图象的顶点M,N关于点P对称.
由题意得$M(-1,-2)$.
如图,连结MN交x轴于点P,分别过M,N作$MA\perp x$轴,$NB\perp x$轴,垂足分别为点A,B,则$MP = NP$,$\angle MAP=\angle NBP = 90^{\circ}$,$MA = 2$.

在$\triangle APM$和$\triangle BPN$中,$\begin{cases}\angle MAP=\angle NBP\\\angle APM=\angle BPN\\MP = NP\end{cases}$
∴$\triangle APM\cong\triangle BPN(AAS)$,
∴$NB = AM = 2$.
对于$y_1=\frac{1}{4}(x + 1)^2-2$,当$y = 2$时,$\frac{1}{4}(x + 1)^2-2 = 2$,解得$x_1 = 3$,$x_2=-5$(舍去),
∴点N的坐标为$(3,2)$.
∵点N是二次函数$y_2$的图象的顶点,
∴可设$y_2=a(x - 3)^2+2(a\neq0)$.把$M(-1,-2)$的坐标代入$y_2=a(x - 3)^2+2$,得$-2=a×(-1 - 3)^2+2$,
解得$a=-\frac{1}{4}$,
∴二次函数$y_2$的表达式为$y_2=-\frac{1}{4}(x - 3)^2+2$.
变式3 -1 [解]
(1)4
(2)
∵旋转前后的两个函数互为“顶点相容函数”,
∴二次函数$y_2$图象的顶点N必在二次函数$y_1=\frac{1}{4}(x + 1)^2-2$的图象上,
∵二次函数$y_2$的图象是由二次函数$y_1=\frac{1}{4}(x + 1)^2-2$的图象绕点P旋转$180^{\circ}$得到的,
∴这两个函数图象的顶点M,N关于点P对称.
由题意得$M(-1,-2)$.
如图,连结MN交x轴于点P,分别过M,N作$MA\perp x$轴,$NB\perp x$轴,垂足分别为点A,B,则$MP = NP$,$\angle MAP=\angle NBP = 90^{\circ}$,$MA = 2$.

在$\triangle APM$和$\triangle BPN$中,$\begin{cases}\angle MAP=\angle NBP\\\angle APM=\angle BPN\\MP = NP\end{cases}$
∴$\triangle APM\cong\triangle BPN(AAS)$,
∴$NB = AM = 2$.
对于$y_1=\frac{1}{4}(x + 1)^2-2$,当$y = 2$时,$\frac{1}{4}(x + 1)^2-2 = 2$,解得$x_1 = 3$,$x_2=-5$(舍去),
∴点N的坐标为$(3,2)$.
∵点N是二次函数$y_2$的图象的顶点,
∴可设$y_2=a(x - 3)^2+2(a\neq0)$.把$M(-1,-2)$的坐标代入$y_2=a(x - 3)^2+2$,得$-2=a×(-1 - 3)^2+2$,
解得$a=-\frac{1}{4}$,
∴二次函数$y_2$的表达式为$y_2=-\frac{1}{4}(x - 3)^2+2$.
查看更多完整答案,请扫码查看


